偷偷借一下老王老師在
http://tw.myblog.yahoo.com/oldbl ... &l=f&fid=30 的圖來說明~~~

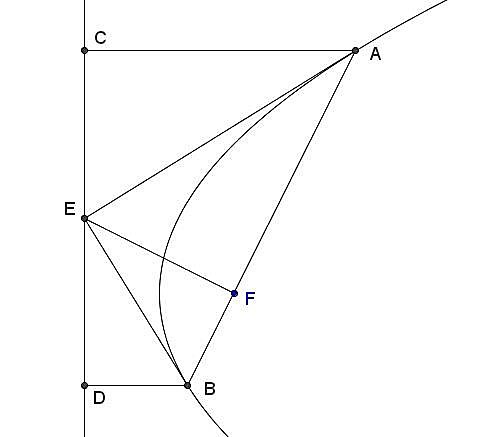
見上圖,自拋物線上一點 \(A\) 做切線 \(\overleftrightarrow{AE}\)(此切線交準線於 \(E\) 點),
自 \(A\) 往準線做垂線,得垂足 \(C\),
設拋物線焦點 \(F\),
由拋物線定義可得 \(\overline{AC}=\overline{AF}\),
由光學性質可推得 \(\angle FAE=\angle CAE\)
再加上 \(\overline{AE}=\overline{AE}\)
可得 \(\triangle FAE\sim\triangle CAE\)
進而可推知 \(F,C\) 兩點會對稱於 \(\overleftrightarrow{AE}\)
亦即,將焦點對稱切線後,對稱點會落在準線上。