引用:

原帖由 jmfeng2001 於 2012-6-20 08:47 PM 發表
不好意思...
想請問計算證明第三題...
是否是用數學歸納法...
但是...最後一步...想不出來...
想請教各位先進
謝謝

計算三：
已知\( a_0=1 \)，且\( \displaystyle a_n=\frac{a_{n-1}}{1+a_{n-1}^2} \)，其中\( n \)為任意正整數。試證：\( \displaystyle a_n \le \frac{3}{4 \sqrt{n}} \)，\( n \in N \)。
[解答]
我的方法參考看看  (我算了我總分扣填充題的得分,發現我這題應該有拿到分數)
\( \displaystyle a_{k+1}=\frac{a_k}{1+a_k^2}<\frac{\displaystyle \frac{3}{4 \sqrt{k}}}{1+\left( \displaystyle \frac{3}{4 \sqrt{k}} \right)^2}=\frac{12}{\displaystyle 16 \sqrt{k}+\frac{9}{\sqrt{k}}}<\frac{12}{16\sqrt{k+1}} \)
＜處，需再證：\( \displaystyle (16\sqrt{k}+\frac{9}{\sqrt{k}})-(16\sqrt{k+1})>0 \)
使用基本微分，即可證明

填充第二題：
設\( \displaystyle f(x)=\frac{1+x}{1-3x} \)。令\( f_1(x)=f(f(x)) \)，且\( f_n(x)=f(f_{n-1}(x)) \)，\( n \ge 2 \)且\( n \in N \)，則\( f_{2012}(2012) \)之值為　　　。
[解答]
\( \displaystyle f_1(x)=\frac{1+f(x)}{1-3f(x)}=\frac{1-x}{-1-3x} \)，\( \displaystyle f_2(x)=\frac{1+f_1(x)}{1-3f_1(x)}=x \)，\( \displaystyle f_3(x)=\frac{1+f_2(x)}{1-3f_2(x)}=f(x) \)，…
每三個一循環，故\( f_{2012}(x)=f_2(x)=x \)


填充第三題：
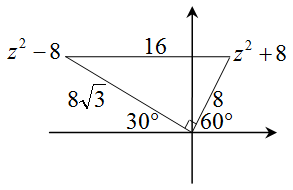
若\( z \)為複數，\( \displaystyle arg(z^2-8)=\frac{5 \pi}{6} \)，\( \displaystyle arg(z^2+8)=\frac{\pi}{8} \)，則\( z \)之值為　　　。
[解答]
\( z^2+8=(a+bi)^2+8=8(cos 60^\circ+i sin 60^\circ) \)　即可解出\( z \)

填充第3題.gif (2.87 KB)

2014-11-22 07:15

填充第四題：
在袋中有紅球、白球各100個，每次從中取出一個球，若為紅球即得1分，白球不計分，滿足下列任一條件即停止：(1)得分達5分，(2)取出球數達10個。試問取球過程會出現幾種不同的方法？　　　。
[解答]
(5紅)+(球數達10顆)\( =[C_4^4+C_4^5+C_4^6+C_4^7+C_4^8+C_4^9]+[C_0^{10}+C_1^{10}+C_2^{10}+C_3^{10}+C_4^{10}]=638 \)

有高手可以幫忙解答第一題嗎?   orz