填充第 5 題相關題目與資料~
利用本站右上角的 Google 自訂搜尋框~
搜尋「三條平行線 正三角形」就可以找到了~:)
https://math.pro/db/thread-890-1-1.html
填充第 5 題:

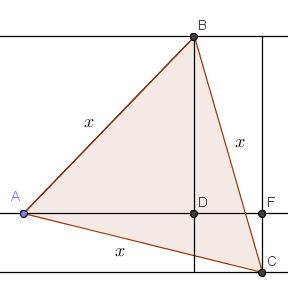
如上圖,設 \(\overline{BD}=d_1, \overline{CF}=d_2\)(不失一般性,假設 \(d_1\geq d_2\))
設正三角形 \(\triangle ABC\) 的邊長為 \(x\),
則由畢氏定理,可得
\(\overline{AD}=\sqrt{x^2-d_1^2}, \overline{AF}=\sqrt{x^2-d_2^2}, \overline{DF}=\sqrt{x^2-\left(d_1+d_2\right)^2}\)
因為 \(\overline{AD}+\overline{DF}=\overline{AF}\)
所以 \(\sqrt{x^2-d_1^2}+\sqrt{x^2-\left(d_1+d_2\right)^2}=\sqrt{x^2-d_2^2}\)
移項平方化簡(做兩次),即可得 \(\displaystyle x^2=\frac{4}{3}\left(d_1^2+d_1d_2+d_2^2\right)\)
\(\displaystyle\Rightarrow x=\frac{2\sqrt{d_1^2+d_1d_2+d_2^2}}{\sqrt{3}}\)