第 7 題：

假設小布走路 \(x\) 公里，阿丹走路 \(y\) 公里，

則小布騎馬 \(n-x\) 公里，阿丹騎馬 \(n-y\) 公里，

\(\Rightarrow (n-x)+(n-y)=n\Rightarrow x+y=n\)

利用小布所花時間＝阿丹所花時間（小時）

可得 \(\displaystyle \frac{x}{4}+\frac{n-x}{6}=\frac{y}{2.5}+\frac{n-y}{6}\)

將 \(n=x+y\) 帶入上式，可得 \(\displaystyle \frac{x}{4}+\frac{y}{6}=\frac{y}{2.5}+\frac{x}{6}\)

\(\displaystyle\Rightarrow y=\frac{5}{14}x\)

因為栓馬點與 \(n\) 都是整數，所以 \(n-x,n-y\) 為整數，可得 \(x,y\) 都為整數，

\(\displaystyle\Rightarrow y=\frac{5}{14}x\Rightarrow x:y=14:5\)

令 \(x=14m, y=5m\) 則 \(n=19m\)，其中 \(m\) 為自然數，

當 \(m=1\) 時，可得 \(n\) 有正整數最小值為 \(19\)，

此時，花費時間\(\displaystyle=\frac{x}{4}+\frac{y}{6}=\frac{13}{3}\)（小時），

所求，\(\displaystyle n+t=13+\frac{13}{3}\cdot60=279.\)

第 8 題：

pentagon.png (33.13 KB)

2012-3-26 11:30

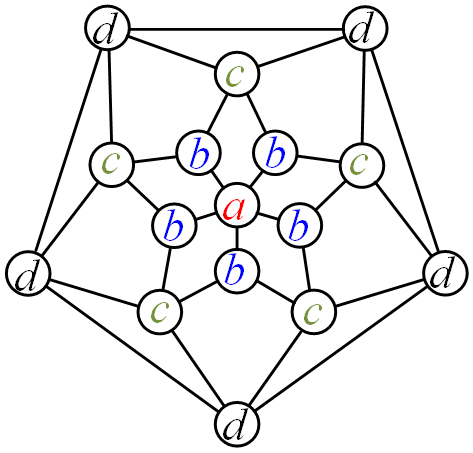
如上圖，設由內往外各節點位置分別持有硬幣數為 \(a,b,c,d\)，則 \(a+5b+5c+5d=3360\)

在最中心位置的同學，經一次交換之後，

自己的 \(a\) 個硬幣全部送出去，流入的硬幣數為 \(\displaystyle 5\cdot \frac{b}{3}\) 個，

因交換前後硬幣數量不變，可列式得 \(\displaystyle a=5\cdot\frac{b}{3}\)

其餘同理可列式得 \(\displaystyle b=\frac{a}{5}+2\cdot\frac{c}{4}, c=2\cdot\frac{b}{3}+2\cdot\frac{d}{4}, d=2\cdot\frac{c}{4}+2\cdot\frac{d}{4}\)

由以上方程式，可解得 \(a=280, b=168,c=d=224.\)

難不難很難說（畢竟有時候某些人突然想到某些特定點～或許就覺得變簡單了～：Ｐ）～

小弟也是有空才看看想想～～哈

不然我提供一個還沒想完～不知要怎樣接續完整的最初的想法，

您可以一起想看看怎樣接續下去好了。

第 13 題假設由原點開始共經過 \(a,b,c,d\) 次的第一、二、三、四種跳動，

而後到達 \((x,y)\) 點，可將 \(x,y\) 以 \(a,b,c,d\) 來表示，

然後找看看 \(x,y\) 有沒有必定要滿足何種規律，

而且能否證明滿足該特定規律的點，可以經由有限次的題敘中的跳動而得。

如果可以處理完上面這段，應該就會變得容易了，

這大概就是小弟的初始想法。：Ｐ

那到底是蝦咪規律呢？慢慢想囉～

（也有可能～想到最後才發現根本不是這個方向也說不一定～：Ｐ）

題目有寫「第一次相遇」時，

此時即是當 n 有「最小整數值」時。

因為圖形旋轉後，會與原圖形相同~

或是你也可以假設 \(16\) 個變數，然後列出更多的方程式，

也可以知道很多變數位置互換後，方程式沒變。