有朋友問我團體賽的第 3,5,6 題，幫他解答後，順便附在這裡～


第 3 題：

\(\displaystyle \left\{\begin{array}{c}f(n)>f(n+1)\\ f(n)>f(n-1)\end{array}\right.\)

\(\displaystyle \Leftrightarrow \left\{\begin{array}{c}f(n)-f(n+1)>0\\ f(n)-f(n-1)>0\end{array}\right.\)

\(\displaystyle \Leftrightarrow \left\{\begin{array}{c}(n+1)0.91^n-(n+2)0.91^{n+1}>0\\ (n+1)0.91^n-n\cdot0.91^{n-1}>0\end{array}\right.\)

\(\displaystyle \Leftrightarrow \left\{\begin{array}{c}0.91^n\left((n+1)-(n+2)\cdot0.91\right)>0\\ 0.91^{n-1}\left((n+1)0.91-n\right)>0\end{array}\right.\)

\(\displaystyle \Leftrightarrow \left\{\begin{array}{c}(n+1)-(n+2)\cdot0.91>0\\ (n+1)0.91-n>0\end{array}\right.\)

\(\displaystyle \Leftrightarrow \left\{\begin{array}{c}n>\frac{82}{9}\\ n<\frac{91}{9}\end{array}\right.\)

因為 \(n\) 為正整數，所以 \(n=10.\)






第 5 題：

如果畫出外接圓圓心，然後連接到題目所給的六邊形的各頂點，把它切割成六個小三角形，

可以發現這六個小三角形重新排列成~邊長依序為 \(4,6,4,6,4,6\) 的新的六邊形的話，則新六邊形的面積不變，

而重排之後的新六邊形面積就好算了，

就將邊長為 \(6\) 的三邊延長，

qq5.png (16.75 KB)

2012-2-20 10:23

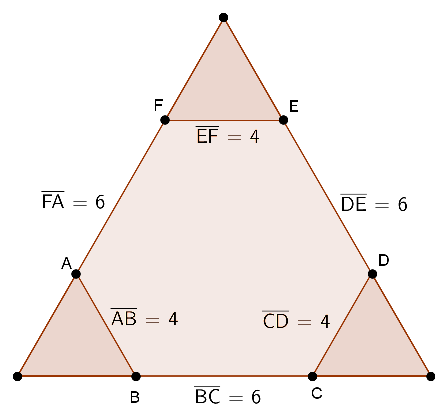
如附圖，用邊長為 14(=4+6+4) 的大正三角形面積扣掉三個邊長為 4 的小三角形面積就可以得到了。

所求面積＝\(\displaystyle \frac{\sqrt{3}\cdot 14^2}{4}-3\times\frac{\sqrt{3}\cdot 4^2}{4}=37\sqrt{3}.\)


ps. 至於為何此新的大六邊形的每個內角都是 \(120^\circ\) ，
　　其實畫出它的外接圓與圓心就可以證的出來了，在此就省略說明了。



第 6 題

設 \(g(x)=ax^2+bx+c,\)

將 \(1,3,4,p\) 分成兩數、兩數為一組～共兩組，

必存在有某一組兩數帶入 \(g(x)\) 得 \(ax^2+bx+c = k_1\)

另一組兩數帶入 \(g(x)\) 得 \( ax^2+bx+c = k_2\)

其中 \(k_1, k_2\) 為 \(f(x)=0\) 的兩根



因此，\(1,3,4,p\) 中的某兩數為 \(ax^2+bx+(c - k_1)=0\) 的兩根，而另兩數為 \(ax^2+bx+(c - k_2)=0\) 的兩根

因為此兩方程式有相同的「兩根之和」，因此有下列三種可能性：

case i: \(1+3=4+p\)

case ii: \(1+4=3+p\)

case iii: \(4+3=1+p\)

可得 \(p\) 的最大值為 \(6.\)

個人賽第 2 題：

因為 \(a+b+c = 9\) ，所以 \(a+b = 9-c\)

所以題目等同於要找 \(c\) 的最小值

再來先換成兩個變數就好~ \(a+b+c= 9\Rightarrow b= 9-a-c\)

帶入 \(ab+bc+ca=0\Rightarrow c(a+b) + ab =0\)

可得 \(c(9-c) + a(9-a-c)=0\Rightarrow a^2 + (c-9) a + c(c-9)=0\)

（上面那行～是刻意表示成 \(a\) 的一元二次方程式的樣子）

因為 \(a\) 為實數，所以上式 \(a\) 的一元二次方程式有實根

由判別式 \(\geq 0\)

可得 \((c-9)^2 - 4\cdot1\cdot c(c-9)\geq 0\Rightarrow -3\leq c\leq 9\)

（討論至此發現，發現 \(c\) 有下界 \(-3\)，但它會是最小值嗎？）

當 \(c=-3\) 時，帶入 \(a^2 + (c-9) a + c(c-9)=0\)

即可解得 \(a = 6\)，

順便再由 \(a+b+c=9\)，可得 \(b = 6.\)

因此，可知當 \((a,b,c)=(6,6,-3)\) 時，

\(c\) 會有最小值為 \(-3\)，

且 \(a+b\) 的最大值為 \(12.\)








個人賽第 9 題：

\(a_1+a_2+a_3+\cdots+a_{2011}=2012\)

\(\displaystyle \frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\cdots+\frac{1}{a_{2011}}=2012\)

如果說要求 \(\displaystyle a_i+\frac{1}{a_i}\) 範圍

可將上面兩式改寫成

\(a_1+a_2+a_3+\cdots+a_{i-1}+a_{i+1}+\cdots+a_{2011}=2012-a_i\)

\(\displaystyle \frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\cdots+\frac{1}{a_{i-1}}+\frac{1}{a_{i+1}}+\cdots+\frac{1}{a_{2011}}=2012-\frac{1}{a_i}\)


由柯西不等式可得

\(\displaystyle \left(a_1+a_2+a_3+...+a_{i-1}+a_{i+1}...+a_{2011}\right)\left(\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\cdots+\frac{1}{a_{i-1}}+\frac{1}{a_{i+1}}+\cdots+\frac{1}{a_{2011}}\right)\)

　　\(\geq \left(1+1+1+....+1+1+1\right)^2\)

\(\displaystyle\Rightarrow \left(2012-a_i\right)\left(2012-\frac{1}{a_i}\right)\geq 2010^2\)

\(\displaystyle\Rightarrow 2012^2 - 2012\cdot a_i - \frac{2012}{a_i} +1 \geq 2010^2\)

\(\displaystyle a_i+\frac{1}{a_i}\leq \frac{8045}{2012}\)

且當等號成立時，\(a_1=a_2=a_3=\cdots=a_{i-1}=a_{i+1}=\cdots=a_{2011}\)

此時，\(2010a_1+a_i=2012\) 且 \(\displaystyle  \frac{2010}{a_1}+\frac{1}{a_i}=2012\)

將「\(a_i\) 帶入 \(a_1\)」或是「\(a_1\) 帶入 \(a_i\)」，再利用根與係數關係式，

皆可討論得 \(a_i\) 與 \(a_1\) 都有正實根，

因此 \(\displaystyle a_i+\frac{1}{a_i}\) 的最大值為 \(\displaystyle \frac{8045}{2012}\)