填充第 13 題
\( n \)為四位數，且各位數字和恰為12，試求\( n \)有幾個？
[解答]
設此四位數的千、百、十、個位分別為 \(a,b,c,d\)

則 \(a+b+c+d=12\)

其中 \(1\leq a\leq 9,\, 0\leq b\leq 9,\, 0\leq c\leq 9,\, 0\leq d\leq 9\)


所求＝\(H_{11}^4-C^3_1 H_1^4 -C^1_1 H_2^4 = 342\)

（註：任意－\(b,c,d\)某個爆掉－\(a\)爆掉 ）

以 \(b\) 爆掉為例，

若 \(b\geq10\) 就會爆掉，

此時 \(a+b+c+d=12\)，

其中 \(a\geq1, b\geq10, c\geq0, d\geq0\)，且 \(a,b,c,d\) 為整數，

滿足此條件的解共有 \(H^4_{12-1-10}=H^4_1\) 種情況。

且因為全部和也才 \(12\)，因此 \(b,c,d\) 不可能有兩個以上同時爆掉，

所以 "不用" 再加回來兩個以上同時爆掉的情況！

填充第2題
設橢圓\( \displaystyle \Gamma：\frac{(x-3)^2}{98^2}+\frac{(y-16)^2}{2009^2}=1 \)，且其內部於第一、二、三、四象限內所圍區域面積依次為\( R_1、R_2、R_3、R_4 \)，則\( R_1-R_2+R_3-R_4= \)　　　。
[解答]
由圖形的對稱性可知，

\(R_1-R_2+R3-R4=\) 附圖的中間白色區域面積\(=4(3\times16)=192.\)

填充第 5 題
若\( \displaystyle k=1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}+\frac{1}{\sqrt{5}}+\ldots+\frac{1}{\sqrt{80}} \)，求\( \left[ k \right]= \)　　　。(\( \left[ \right] \)表高斯符號)
[解答]
很多學校有考過

https://math.pro/db/thread-156-1-1.html

https://math.pro/db/thread-1095-1-1.html

第 12 題：
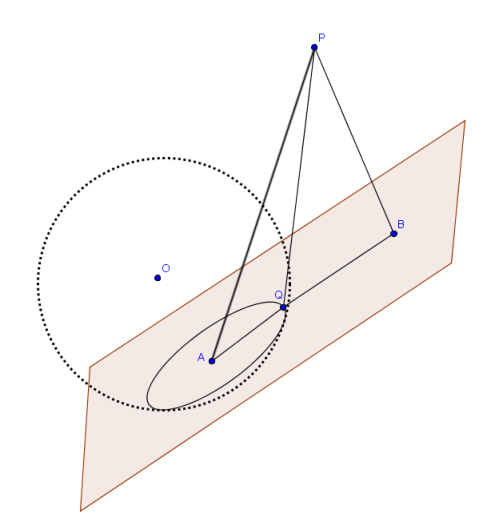
設\( P(4,3,1) \)，\( \displaystyle \Gamma：\cases{x^2+(y-1)^2+(z-5)^2=13 \cr x+2y+2z=3} \)，\( Q \)為\( \Gamma \)上的一動點，求\( \overline{PQ} \)的最小值=　　　。
[解答]
先求出球心 \(O(0,1,5)\) 在平面 \(x+2y+2z-3=0\) 上的投影點坐標 \(A(-1,-1,3)\)，\(A\) 點即 \(\Gamma\) 所表示的圓之圓心，

再求出 \(\Gamma\) 所表示的圓半徑 \(\displaystyle r=\sqrt{13-\left(\frac{|0+2+10-3|}{\sqrt{1^2+2^2+2^2}}\right)^2}=2\)

然後，求出 \(P(4,3,1)\) 在平面 \(x+2y+2z-3=0\) 上的投影點坐標亦為 \(B(3,1,-1)\)，

且 \(P(4,3,1)\) 到平面 \(x+2y+2z-3=0\) 的距離為 \(\displaystyle \overline{PB}=\frac{|4+6+2-3|}{\sqrt{1^2+2^2+2^2}}=3\)

可得 \(\overline{AB}=6\)，

\(\overline{PQ}\) 的最小值為 \(\displaystyle \sqrt{\overline{PB}^2+\left(\overline{AB}-r\right)^2}=5.\)

註：這也是考古題，以前其他學校有出過（忘了哪幾所～）。

因為小弟記憶力太弱～所以不太會背公式，又擔心背錯～常每次都用推導的～

你上面回覆的公式是套用哪一個呢？（因為我看不太出來...＝＝）

如果是套用我之前寫的積分的方法～得到的是 \(2\left(\sqrt{81}-1\right)<k<1+\frac{1}{\sqrt{2}}+2\left(\sqrt{80}-\sqrt{2}\right)\)

\(\Rightarrow 16<k<16.76...\Rightarrow [k]=16\)

如果是套用後面 bugmens 所提供的方法（較常見）～得到的是

\(1+2\left(\sqrt{81}-\sqrt{2}\right)<k<1+2\left(\sqrt{80}-\sqrt{1}\right)\)

\(\Rightarrow 16.17...<k<16.88...\Rightarrow [k]=16\)



不過，由於您的答案少 \(1\) ～我猜你是用後者～～

然後我猜你的錯誤點很有可能是～\(1\) 本身已是整數不需要處理～卻不小心也拿進去分項對消處理了！

填充第 3 題
主人宴客，刻意安排10個互不認識的客人一同圍坐一圓桌，希望客人能互相認識，不料席間每位客人都只與相鄰的人交談認識。飯局後主人從中隨意挑選四人, 試求四人皆互不認識的機率？　　　。
[解答]
我也來個另解好了，原理跟老王老師的差不多（把圍圈圈剪開變成直線排列）~

將環繞一圈的賓客依序編號為1,2,...,10號

分母＝由1~10號任取四個號碼＝\(C^{10}_4=210\)

分子＝n（由1~10號任取四個號碼，任兩號碼不連續，且1與10不同時出現）

　　＝n（由1~10號任取四個號碼，任兩號碼不連續）－n（由1~10號任取四個號碼，任兩號碼不連續，且1與10同時出現）

　　＝\(C^7_4 - C^2_2\cdot C^5_2\)

　　＝\(25\)

註：\(C^7_4\) 說明～～～10個號碼要選四個○　→　不要選的有六個●，把這六個用●●●●●●表示

　　要選取的號碼～～就是在六個●所區隔出來的七個空隙之中選取四個放○，因此有 \(C^7_4\) 種選取的方法。

　　\(C^2_2\cdot C^5_4\) 說明～～～同上，但是頭尾兩個空隙一定要選○，剩下中間五個空隙要選兩個來放○。

那我試圖寫一個作法~使得答案剛好是 \(\displaystyle [H(4,2)*3!*6!]/(9!) = \frac{H^4_2}{C^9_3}\) 看看。

先固定某一人一定會選取到，剩下九人任取三人，

看剩下九人任取三人的所有情況中，有多少種會使得全部取出來的四人不相鄰，

以○表示被選取出來的人，以●表示沒有被選取出來的人，

因為被選取出來的人有四位，且每兩位中間都要間隔一個●，

且繞成圈圈也要使得頭尾的○不相鄰，所以尾巴多放一個●

因此排成一直線是　○●○●○●○●

由剩下兩個●●要放入上列中四個"●"所在的區塊中，可能的方法數為 \(H^4_2\)

放進去之後，由左到右，第一個○就是一開始被選定的人，剩下的○就是其他被選出來的人所在的位置。

所以，所求機率＝\(\displaystyle \frac{H^4_2}{C^9_3}\)

再來解釋一下「7個直線不相鄰，用剩下4個去隔開，所以是C(5,3)」

第一個任取，馬上可以知道他的左右兩邊不能取，

所以「剩下七個人要選出不相鄰的三個」，

不被選出來的有四個，要被選出來的有三個，且要被選出來的不能相鄰，

相當於四個●●●●跟三個○○○排成一直線，但是三個○中任兩個都不相鄰，

先排四個●●●●，排完之後，要把三個○放入四個●所隔開的五個空隙中的某三個空隙，

所以方法數有 \(C^5_3\)