一個四面體的每一個面都是邊長分別為6,9,9的三角形,求該四面體體積
。
[解答]

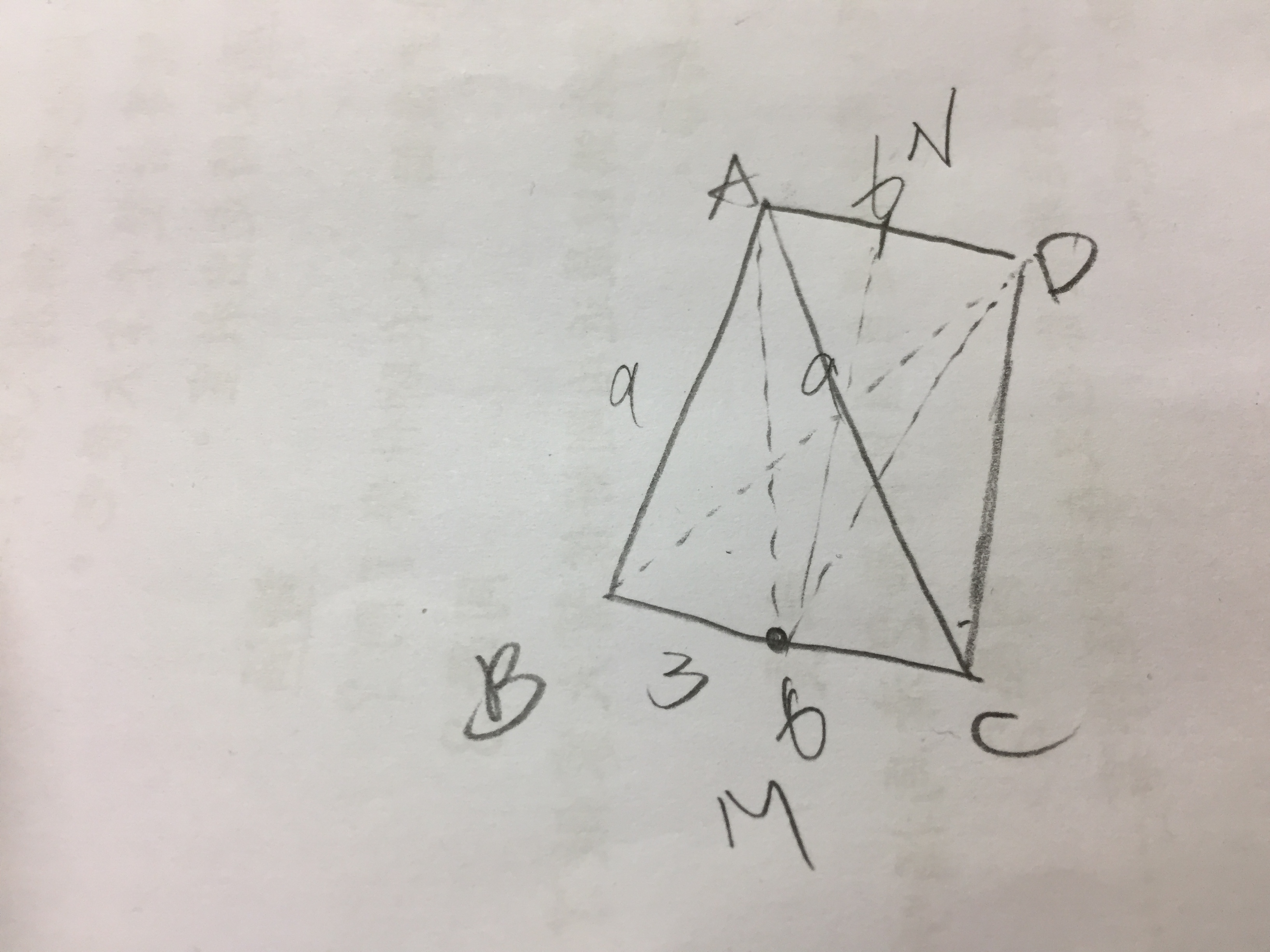
畫出來,四個面都會是等腰三角形
設\(\overline{BC}\)中點為\(M\)、\(\overline{AD}\)中點為\(N\)、高為\(h\)
則\(\overline{AM}=\overline{DM}=6\sqrt{2}\),因為都是等腰三角形,所以\(A\)到底面積的高,垂足會落在\(\overline{BD}\)上,先可得到\(\overline{MN}=3\sqrt{7}\)
\(\displaystyle\frac{\overline{DM}\times h}{2}=\frac{6\times\overline{MN}}{2}\rightarrow h=\displaystyle\frac{3\sqrt{7}}{\sqrt{2}}\)
體積就可以直接算,\(V=\displaystyle\frac{1}{3}\times 6\times 6\sqrt{2}\times\frac{3\sqrt{7}}{\sqrt{2}}\times \frac{1}{2}=18\sqrt{7}\)