原來如此,感謝cefepime 大大的解說!您的想法讓小弟讚嘆不已!
PS:5/4會備份主機大家要留意ㄧ下板上資訊
4.
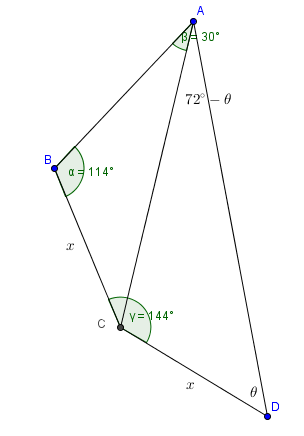
四邊形\(ABCD\)中,\(\overline{BC}=\overline{CD}\),\(\angle ABC=114^{\circ}\),\(\angle BCD=144^{\circ}\),\(\angle BAC=30^{\circ}\),則\(\angle ADC=\)
[解答]
\(
\begin{array}{l}
\left\{ \begin{array}{l}
\displaystyle \frac{x}{{\sin 30^{\rm{^\circ }} }}=\frac{{\overline {AC} }}{{\sin 114^{\rm{^\circ }} }} \\
\displaystyle \frac{x}{{\sin (72^{\rm{^\circ }} - \theta )}}=\frac{{\overline {AC} }}{{\sin \theta }} \\
\end{array} \right. \\
\displaystyle 2\sin (72^{\rm{^\circ }} - \theta )\sin 114^{\rm{^\circ }} = \sin \theta \\
\displaystyle 2\sin (72^{\rm{^\circ }} - \theta )\cos 24^{\rm{^\circ }} = \sin \theta \\
\theta = 48^{\rm{^\circ }} \\
\end{array}
\)
第九題
9.
求不等式\(-3<\left[|\;x-1|\;-6\right]<3\)的解為
。(\(\left[x\right]\)表不大於\(x\)之最大整數)
[解答]
\(高斯函數
[x] \le x{\rm{ < [}}x{\rm{] + 1}}
\)
\(
\begin{array}{l}
{\rm{[| }}x - 1{\rm{ |}} - 6{\rm{] = }} - 2, - 1,0,1,2 \\
- 2 \le {\rm{| }}x-1{\rm{ |}} - 6{\rm{ < 3}} \\
5 \le x<10, -8<x \le -3 \\
\end{array}
\)