若
x 為自然數,定義
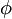 (x)
(x) 為不大於
x 且與
x 互質的自然數個數.
此為 Euler 的 phi function,基礎數論的書都會提到。
第一小題:
先證 Euler's phi function 是 multiplicative 的算數函數(亦即,對互質的自然數
m n
n 恆有
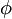 (mn)=
(mn)=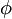 (m)
(m)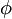 (n)
(n)),
接著就可以容易推得該結論。
詳見:
http://math.ntnu.edu.tw/~li/ent-html/node11.html
第二小題:
Key:若
a 是小於
x 且與
x 互質的數,則
x−a 亦是。