




| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| \(f(n)\) | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 |
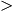 0 恒成立。
0 恒成立。原帖由 weiye 於 2010-6-22 02:32 PM 發表
演算題第 4 題:
245
如圖,在座標平面上,將橢圓 \(\displaystyle\frac{x^2}{4}+\frac{y^2}{1}=1\) 的上半部及圓 \(x^2 + y^2 = 4\) 的下半部組合而成一封閉曲線(其中, \(A, B\) 為此橢圓與圓的交點)。
今有一光線從此 ...
原帖由 idontnow90 於 2010-7-9 11:08 AM 發表
想請教第7題...為什麼-------則對任意實數 t,f(t)0 恒成立。
\(det(A) \neq 0\) will imply det(A) > 0 ???
謝謝~ ...
原帖由 八神庵 於 2010-7-8 08:13 PM 發表
你被垂心騙了,這題的重點在角A=60度
令AC=b,AB=c
在三角形ACF中,AF=ACcos60度=b/2,AE=ABcos60度=c/2
因為角AFP=角AEF=90度,由四邊形內角和可知角FPE=120度
因此
三角形ACF,三角形ABE,三角形BFP與三角形CEP均為30-60 ...

原帖由 kittyyaya 於 2010-8-26 06:34 PM 發表
請問最後一句"由邊長比再搭配畢氏定理可以算出c與FP",邊長是那個比那個,
因為我一直算出2b=c+6而已,找不到第二個方程式,可以麻煩在多點說明嗎?謝謝 ...
原帖由 weiye 於 2010-8-26 07:27 PM 發表
填充第 4 題:右圖是某次期中考,隨機抽樣調查高三 \(20\) 位同學 \(A,B,\cdots,T\) 等人的國文、英文成績所畫出的散佈圖。對這 \(20\) 位學生,算出每個人的國文、英文兩科的平均成績(即相加再除以 \(2\) )。請問,哪個人 ...
| 歡迎光臨 Math Pro 數學補給站 (https://math.pro/db/) | 論壇程式使用 Discuz! 6.1.0 |