引用:
原帖由 weiye 於 2008-5-6 08:31 PM 發表
第一式:
由左式開始,將第一、二、三、四行分別提出 a_1, a_2, a_3, a_4,
然後將第一行乘以 -1 倍加到第二、三、四行,
沿第一列展開,得一個三階行列式,
將此三階行列式沿各行各列,將分母都提出來,
即可得右式。
所以,第一 ...

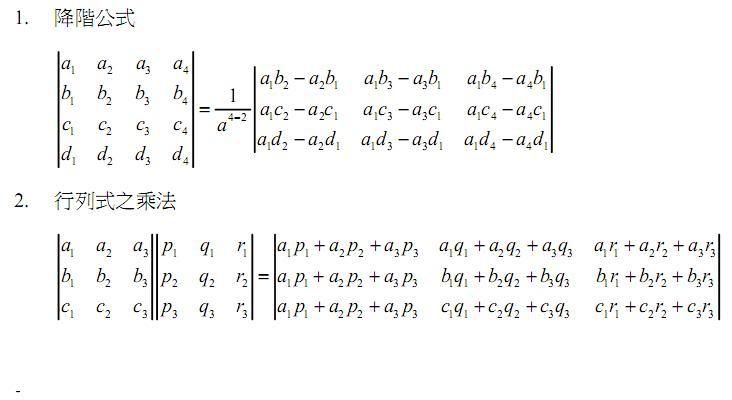

原帖由 weiye 於 2008-5-6 08:31 PM 發表
第一式:
由左式開始,將第一、二、三、四行分別提出 a_1, a_2, a_3, a_4,
然後將第一行乘以 -1 倍加到第二、三、四行,
沿第一列展開,得一個三階行列式,
將此三階行列式沿各行各列,將分母都提出來,
即可得右式。
所以,第一 ...
| 歡迎光臨 Math Pro 數學補給站 (https://math.pro/db/) | 論壇程式使用 Discuz! 6.1.0 |