
標題: 算幾不等式一問 [打印本頁]
作者: smartdan 時間: 2013-5-22 22:44 標題: 算幾不等式一問
設 0<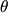 <π/2,求 9 tan^2θ+ 4 cot^2θ+ 12 tanθ+12 cotθ 的最小值
<π/2,求 9 tan^2θ+ 4 cot^2θ+ 12 tanθ+12 cotθ 的最小值
這題我是用這四項下去做算幾
因為我想到
tan^2θ x cot^2θ x tanθ x cotθ = 1
(9 tan^2θ+ 4 cot^2θ+ 12tanθ+12 cotθ)/4≧
(9tan^2θ x 4 cot^2θ x 12tanθ x 12 cotθ)^ 1/4
但是詳解是拆成兩組去做兩個算幾
(9 tan^2θ + 6 cotθ + 6cotθ) / 3 +(4 cot^2θ+6tanθ+ 6tanθ) / 3≧
(9 tan^2θ x 6 cotθ x 6cotθ)^ 1/3 +(4 cot^2θ x 6tanθ x 6tanθ)^ 1/3
可以請問一下各位先進,為什麼我的方法是錯誤的?
作者: weiye 時間: 2013-5-22 23:07 標題: 回復 1# smartdan 的帖子
你找出來的是下界,因為你還沒有檢查"等號"是否會成立。
找出來的「上界(or 下界)」不一定就會是「最大值(or 最小值)」,
還要檢查「等號是否有可能成立」才知道其值是否為最大(或最小)值。
尤其是連續串接好幾個不等式才找到上界(or 下界)時,更要檢查等號是否會同時成立。
ps. 這個觀念在平常教學生不等式的時候,也要常常叮嚀!
例:已知 \(x\) 為 "正整數",易知 \(x\geq -100\)。
提問那是否表示 \(x\) 的"最小值"為 \(-100\)?
作者: smartdan 時間: 2013-5-26 10:01 標題: 回復 2# weiye 的帖子
非常的感謝!!!茅塞頓開
| 歡迎光臨 Math Pro 數學補給站 (https://math.pro/db/) |
論壇程式使用 Discuz! 6.1.0 |

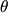 <π/2,求 9 tan^2θ+ 4 cot^2θ+ 12 tanθ+12 cotθ 的最小值
<π/2,求 9 tan^2θ+ 4 cot^2θ+ 12 tanθ+12 cotθ 的最小值