台灣師大96筆試二
h ttp://www.math.ntnu.edu.tw/html/dstg/dstg.htm 連結已失效
h ttp://www.ptt.cc/bbs/Math/M.1231773896.A.1F8.html 連結已失效
空間中位於點(0,2,2)的光源,將xz平面上的圓
x2+(z−1)2=1 , y=0
照射在xy平面上,則這個影像的曲線方程式為
[解答]
x2+(z−1)2=1 , y=0的參數式
(cosθ 0
0 1+sinθ)
(cosθ
1+sinθ)
(cosθ 0
0 1+sinθ)
1+sinθ)和(0 , 2 , 2)的直線參數式
xcosθ=−2y−2=z−2sinθ−1
該直線和z=0的交點
xcosθ=−2y−2=0−2sinθ−1
sinθ=y−2y+2 ,
cosθ=−2xy−2
利用
sin2θ+cos2θ=1,得到
x2+2y=0 , z=0
113.6.8補充
空間中有一光源位於
(0 2
2 2)
2),將
xz平面上的圓
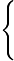 x2+(z−1)2=1y=0
x2+(z−1)2=1y=0 照射在
xy平面上,求此圓在
xy平面上的軌跡方程式
。
(106興大附中,
https://math.pro/db/viewthread.php?tid=2749&page=1#pid17004)