計算題
試求
 10−6cos
10−6cos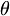 +41
+41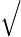 34−24
34−24 2sin
2sin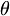 +
+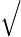 19−2
19−2 2cos
2cos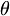 −8sin
−8sin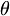
的最小值。
[解答]
原式 = √[(cos θ - 3)^2 + (sin θ)^2] + √[(cos θ)^2 + (sin θ - (3/4) √2)^2] + √[(cos θ - √ 2)^2 + (sin θ - 4)^2]
所求即單位圓上一點到 A( 3,0)、B(0,(3/4) √2)、C(√2,4) 距離和的最小值
直線 AB 和 OC 垂直,垂足 P(1/3,(2/3)√2) 在單位圓上
所求 = PA + PB + PC = AB + OC - 1 = (21/4) √2 - 1