第 3 題
令
f(x)=21+cosx+cos(2x)+

 +cos(10x)
+cos(10x)。
(a)試證明
f(x)=2sin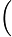 x2
x2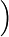 sin
sin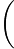 221x
221x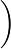
。
提示:用
z=cosx+isinx將
cosx表示成
cosx=2z+z。
(b)在滿足
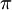 2
2 x
x
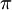
的條件下,試求出方程式
f(x)=0解的個數。
[解答]
(a) z = cosx + isinx = e^(ix)
令
s = 1 + cosx + cos(2x) + ... + cos(10x)
t = 1 + sinx + sin(2x) + ... + sin(10x)
s + it = 1 + e^(ix) + e^(i2x) + ... + e^(i10x)
= [1 - e^(i11x)]/[1 - e^(ix)]
= {[1 - e^(i11x)][1 - e^(-ix)]}/{[1 - e^(ix)][1 - e^(-ix)]}
= [1 - e^(-ix) - e^(i11x) + e^(i10x)]/(2 - 2cosx)
s = 1 + cosx + cos(2x) + ... + cos(10x)
= [1 - cosx - cos(11x) + cos(10x)]/(2 - 2cosx)
= (1/2) - [cos(11x) - cos(10x)]/(2 - 2cosx)
= (1/2) + [2sin(21x/2)sin(x/2)]/4[sin(x/2)]^2
= (1/2) + sin(21x/2)/[2sin(x/2)]
f(x) = s - 1/2 = sin(21x/2)/[2sin(x/2)]
(b) π/2 ≦ x ≦ π
5.25π ≦ (21/2)x ≦ 10.5π
sin(21x/2) = 0,有 5 個解