第 1 題
神童如風參加心算比賽的電視節目錄影,裁判亮出題目,觀眾只理解到題目是求
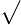 1515
1515 □□□
□□□ □□□
□□□ □□□
□□□ □□□
□□□ □□□
□□□ 這個開根號的數時(方框代表觀眾來不及記憶的數字),說時遲,那時快,如風只花了15秒就算出這個複雜的根式是一個正整數
k,並經裁判確認正確。請問正整數
k= 。
[解答]
根號裡是 17 位數
10^15 是 16 位數
11^15 也是 16 位數
15log12 = 16.1865
12^15 是 17 位數,首位是 1
第 5 題
小美每天早上起床後必先完成洗臉、刷牙、穿衣服、穿裙子、戴隱形眼鏡和吃早餐等六件事情,其中洗臉後才能戴隱形眼鏡,刷牙和洗臉後才會吃早餐,例如:洗臉→穿衣服→穿裙子→刷牙→戴隱形眼鏡→吃早餐。請問小美完成這六件事情,依前後順序的不同,共有
種方法。
[解答]
先排洗臉、戴眼鏡、刷牙、吃早餐
有以下 5 種情形
洗臉、刷牙、吃早餐、戴眼鏡
刷牙、洗臉、吃早餐、戴眼鏡
洗臉、戴眼鏡、刷牙、吃早餐
洗臉、刷牙、戴眼鏡、吃早餐
刷牙、洗臉、戴眼鏡、吃早餐
剩下兩個插空隙
所求 = 5 * H(5,2) * 2
第 8 題
設
A( )
)、
B(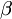 )
)、
C(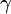 )
)為複數平面上不共線的三點,都不在實軸上,

、
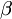
、
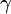
皆不為零,若
AC=4且
 2+4
2+4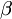 2+5
2+5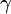 2=2
2=2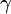 (
( +4
+4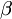 )=
)= 。
[解答]
α^2 + 4β^2 + 5γ^2 = 2γ(α + 4β)
(α - γ)^2 = -4(β - γ)^2
α - γ = ±2i(β - γ)
AC 和 BC 垂直
AC = |α - γ| = |±2i(β - γ)| = 2|β - γ| = 2BC
BC = 2
AB = 2√5