第6題
−1+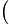 −1+d
−1+d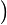 +
+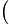 −1+2d
−1+2d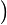 =a−1
=a−1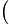 −1
−1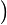
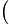 −1+d
−1+d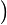
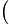 −1+2d
−1+2d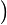 =−2a−5
=−2a−5
解聯立
第8題
△→□→□→□→□→□→△
不管幾個 ↑ 填入某個 □ 中都會產生 2 次轉彎
不管幾個 ↑ 填入某個 △ 中都只會產生 1 次轉彎
恰轉 3 次彎的情形: a 個 ↑ 填入 1個 □ 和 (5 - a) 個 ↑ 填入 1 個 △,1 ≦ a ≦ 4
5個 □ 選一個,2 個 △ 選一個,而a 有 1 ~ 4 這四種情形
故
C15 C12
C12 4=40
4=40
第 10 題
利用 R 在平面 PEQ 上,求出 R 的坐標
如此就有向量 PR 和向量 EQ,再直接求夾角的餘弦值即可
[
本帖最後由 thepiano 於 2020-8-8 07:53 編輯 ]