引用:
原帖由 Superconan 於 2019-8-2 02:13 發表 
請問第 7 題,
我解釋的方法是「若將 AC = 2 代回原本三角形,會發現 ABC 應為等腰直角三角形,但是邊長比不符,所以 AC = 2 不合 。」
不知道有沒有更好的解釋方法?因為若只能將求得的值代回檢驗,我不知道該如何判定 AC = 5/2 是正確答案。.
填充第七題:
前半段利用正弦定理算出
cosC=43,到此作法無誤。
後半段利用
AC 滿足餘弦定理
AC2+32−2 AC
AC 3cosC=22
3cosC=22 尚可,
不至於全然說是錯,只是尚未排除不可能的值....咦?為什麼會產生不滿足條件的值呢?說明如下。
就像 『"
x=3 (x−3)(x−2)=0
(x−3)(x−2)=0" 的逆敘述 "
(x−3)(x−2)=0 x=3
x=3" 不一定成立。』
由餘弦定理,可知
x=AC 滿足條件
x2+32−2 x
x 3cosC=22
3cosC=22 ,
不保證所有滿足條件
x2+32−2 x
x 3cosC=22
3cosC=22 的
x 值都會是
AC,
因為
x2+32−2 x
x 3cosC=22
3cosC=22 是一元二次式方程式,至多有兩個根。
除了求出兩個可能的
x ,再排除不適合的值以外。
比較適合的做法,是在求出
cosC=43 之後,
先求
cosB=cos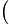 180
180 −
−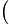
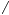 A+
A+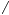 C
C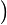
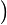 =cos
=cos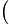 180
180 −3
−3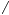 C
C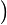 =3cosC−4cos3C=916
=3cosC−4cos3C=916
再利用餘弦定理,得
AC= 22+32−2
22+32−2 2
2 3cosB=25
3cosB=25 。
註:如果不是因為要教三角函數,這題也可以只使用相似三角形就求出來。

