先附三個類題,這三個類題是點 Q 在橢圓內,求相加,但做法一樣,就是利用到兩焦點距離和
=2a 及三角不等式
已知點 P 為橢圓
x264+y228=1 上的點,
A(6 0)
0) B(−3
B(−3 4)
4),求
PA+PB 的最小值為? (100玉井工商)
坐標平面上,已知點 A(4,0) 和 B(3,3),P 是橢圓
x236+y220=1 上的動點,則
PA+PB 的最小值為 __________。 (100彰化女中)
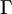 :x216+7y2=1
:x216+7y2=1,
F(3 0)
0) A(−3
A(−3 1)
1),P 在
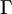
上,設
PA+PF 最大值 M,最小值 m,則 (M,m)=_________。 (99建中市內)
此題解答:
橢圓
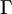 : 7x2+y216=1
: 7x2+y216=1 中,
F 為焦點,其
y 坐標為正。
P(x y)
y) 為
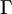
上的動點要
Q(6 5)
5)。試求
PQ−PF 的最小值 __________
解:兩焦點
F(0 3)
3) F
F (0
(0 −3)
−3),
PF=8−PF
。
PQ−PF=PQ+PF −8
−8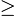 QF
QF −8= 10−8=2
−8= 10−8=2
當
P 為
QF
與
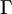
的交點時,達最小值 2。