參考附件

設\(a_n\)表傳球\(n\)次後球在林的方法數
則\( a_7+a_6=4^6 \)，\( a_6+a_5=4^5\) ......\(a_2+a_1=4^1\)，\(a_1=0 \)
=>\( a_7=4^6-4^5+4^4-4^3+4^2-4=3276 \)

\(t^4-zt^3-yt-x=0 \)有\(a,b,c\)三根
=>\( \displaystyle t^4-zt^3-yt-x=(2t^3-2t^2+3t-1) \left( \frac{t}{2}+\frac{3}{4}\right) \)
=>\( \displaystyle x=\frac{3}{4},y=-\frac{7}{4},z=-\frac{1}{2} \)

填充1
感謝laylay老師的說明，小弟另外再補充個作法
題意所求可視為7個區塊(傳7次)，5種不同顏色(人)，相鄰區域不同色，因為必須傳給Lin，故最後一個區域必須固定，故除5
\(
\displaystyle \frac{{(5-1)^7 +(-1)^7(5-1)}}{5} = 3276
\)

填充6 除了三角函數硬爆外，大家有其他想法嗎？

填充7  當A、D、P共線時周長最大


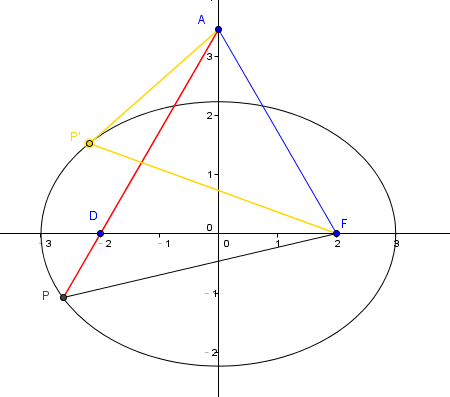
填充8  答案錯了，應該是\(-2\)


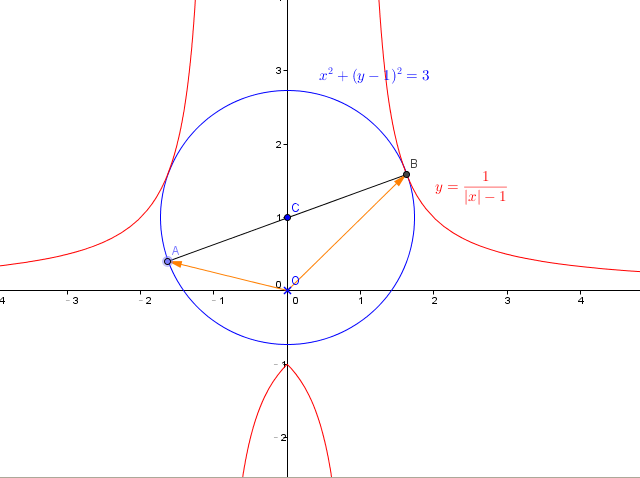
填充13
\(
\displaystyle 一路領先問題 \frac{{C_{51}^{99+51-1+2} +C_{51-1}^{99+51-1+2} }}{{C_{51}^{150} }} = \frac{{151}}{{202}}
\)


計算6
\(
\begin{array}{l}
\displaystyle \left( {\frac{{a^2 }}{{a+3b}}+\frac{{b^2 }}{{a+3b}}+\frac{{b^2 }}{{b+3c}}+\frac{{c^2 }}{{b+3c}}+\frac{{c^2 }}{{c+3a}}+\frac{{a^2 }}{{c+3a}}} \right)\left( {a+3b+a+3b+b+3c+b+ 3c+c+3a+c+3a} \right) \\
\displaystyle  \ge \left( {a + b + b + c + c + a} \right)^2  \\
\end{array}
\)

[ 本帖最後由 eyeready 於 2017-4-27 10:30 編輯 ]

(3/13)*(6/10)(最後為白球)+(6/13)*(3/7)(最後為黑球)=153/455
建議再加5顆黃球,其他不變,有興趣的請討論看看

[ 本帖最後由 laylay 於 2017-4-27 11:05 編輯 ]

第一部分  填充11

11.JPG (90.8 KB)

2017-4-27 12:20

[ 本帖最後由 windin0420 於 2017-4-27 12:23 編輯 ]

想請問填充2.3.6.8.12
填充6...1/2的答案想不出來
填充8...半徑要怎麼算
剩下的完全沒想法
感謝

填充12.

IMG_9124.JPG (643.13 KB)

2017-4-27 18:42

填充第3題
\( \displaystyle f\left( x \right)=\frac{{{x}^{4}}+r{{x}^{2}}+1}{{{x}^{4}}+{{x}^{2}}+1}=1+\frac{\left( r-1 \right){{x}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}\)

\(\left( 1 \right)r=1,f\left( x \right)=1\)，恆成立

\(\begin{align}
  & \left( 2 \right)r>1 \\
& 0\le \frac{{{x}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}\le \frac{1}{3} \\
& 0\le \frac{\left( r-1 \right){{x}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}\le \frac{r-1}{3} \\
& 1\le f\left( x \right)\le \frac{r+2}{3} \\
& 1+1>\frac{r+2}{3} \\
& 1<r<4 \\
&  \\
& \left( 3 \right)r<1 \\
& 0\le \frac{{{x}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}\le \frac{1}{3} \\
& \frac{r-1}{3}\le \frac{\left( r-1 \right){{x}^{2}}}{{{x}^{4}}+{{x}^{2}}+1}\le 0 \\
& \frac{r+2}{3}\le f\left( x \right)\le 1 \\
& \frac{r+2}{3}>0 \\
& \frac{r+2}{3}+\frac{r+2}{3}>1 \\
& -\frac{1}{2}<r<1 \\
\end{align}\)

綜合以上，\(-\frac{1}{2}<r<4\)

懂了,感謝鋼琴和pgcci7339兩位老師