如題:
設稜長為a,如
如何求出r=a/sqrt(6)
謝謝

參考林信安老師的圖，在第 8 頁的例題 2，其中內切球的半徑是 OG，而 G 是正△ADE 的重心
http://www.google.com.tw/url?sa= ... amp;bvm=bv.87519884,d.dGY

謝謝 鋼琴師
為何 G 是正△ADE 的重心?
謝謝

從正六面體(正方體)與其內切球來看是"重心"，正八面體應該也是
不然就定 O(0，0，0)，D(1，-1，0)，E(1，1，0)，A(0，0，√2) 去找切點

既然動了坐標，何不使用點到平面距離公式呢？

那到後面就會用到了

寸絲兄，有不用坐標的說法嗎？

從對稱性的觀點來看，球心只能在正八面體的中心點，切點只能在八個正三角形面的中心(重心)

或者先接受球心只能在正八面體的中心點，令其為 O。 ABC 為正八面體的一面，M 為 BC 中點，P 為球和 ABC 的切點。

則有 OP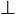ABC 和 OM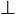BC，由三垂線定理有 PM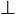BC，故 −PM 為 BC 中垂線(亦為中線)，同理可得 P 在三中線上。

半徑的計算則可由直角 AOM 的面積 21AOOM=21AMOP，其中 OP 為內切球半徑。

各長度以正八面體之邊長表示則得 21a22a=2123ar  r=a6 

謝謝tsusy老師的解釋