將一個球帽型容器裝滿水，其中球的半徑為2，
若球心到球帽上緣所在的平面距離為1，試求此容器的體積。答：9pi
（不會畫立體圖，「球帽」的意思是：完整的球，橫切一刀使截面為圓，並捨棄較小的那塊）
（希望看的懂意思＠＠）

我的作法：
用1/3的球體積（因為角度120度）扣掉圓錐體積，
(1/3)(4pi2^3/3) - (1/3)(3pi)=32pi/9 - pi = 23pi/9
答案不一樣，還是那部份不是1/3呢？
好難想像啊><"

1. 該容器的體積應為 12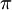(4−x2)dx=35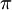  (這個球的體積也才不到 10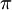 而已)

2. 如果要用角度這樣的想法，必須引進立體角。

一般的角度，是弧長 / 周長。立體則是表面積 / 球的表面積。

3. 如果要直接說 31 為什麼是錯的。可以想像平面上有一個圓，平分成三個圓心角為 120 的扇形。

每個扇心對其圓心角的角平分線旋轉，就是您想像以為是 31 球體積的圖形。

但實際上，這個三個旋轉體，彼此不相交，而且被包含在該球裡。

平面上在三個扇形的兩兩交線處的上、下方，很明顯沒有被這三個旋轉體蓋住，也就是三個組起來是不到一個球。

立體圖不會畫，等樓下的高手來畫吧