想請問今年學測多選第11題 應如何解釋 ?謝謝各位老師

我的想法為：正方形四頂點到中心等距離

設橢圓的方程式為 a2x2+y2b2=1 a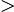b，橢圓的點以參數式表示 P(acos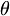bsin)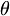

計算其與焦點 F1(c0)  的距離可得 a−ccos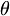

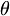
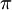
其在 0 中，為遞增函數，因此上半橢圓至少一點為正方形之頂點，下半橢圓亦然

因此至多兩個頂點在楕圓上，上下對稱(正方形擺正)可以剛好兩個，轉 90 讓長軸的端點為正方形的頂點時則為 1 個

正方形很大或很小的話，可以造出 0 個，故答案為 125 (0,1, 或 2個)

[ 本帖最後由 tsusy 於 2013-1-29 11:49 PM 編輯 ]

多選第11題：

取先取個例子：:x225+y216=1，a=5b=4c=3a−c=2ab2=32

選項一：取正方形兩對角線分別平行 xy 軸，且一半的對角線長為 2。

選項二：取正方形兩對角線分別平行 xy 軸，且一半的對角線長為 32。

選項三、四：因為橢圓上至多兩點（此兩點對稱長軸）到 F1 的距離會相同，

　　　　　　所以不可能有三個以上的點到 F1 的距離相同。

　　　　　　（設 P 為 上的定點，而 Q 為 上異於 P 且滿足 PF1=QF1　的動點，

　　　　　　　則 PF2=2a−PF1=2a−QF1=QF2

　　　　　　　且因為 F1F2=F1F2，所以 PF1F2 全等於 QF1F2

　　　　　　　由圖形，可知恰只有一點 Q （PQ 對稱於長軸）滿足上述全等條件～三角形三內角角度唯一確定（F1F2 不可交換位置喔！）～）

選項五：取正方形兩對角線分別平行 xy 軸，且一半的對角線長為 1。

感謝兩位老師解答
寸絲老師 橢圓的參數式在99正綱已經改到高三自然組了 不適合對高三社會組說明
瑋岳老師 您的PF1=QF1 P Q是在正方形的頂點嗎
另外 可以請教各位老師 這題主要考學生的目的何在 開學後不知該如何對學生說明

PQ 是在說明～橢圓上至多兩點到 F1 的距離會相同。

你要把它當頂點也可以，如果有 R 也滿足 RF1=PF1=QF1，

則 R 必定是 P 或 Q 的其中一點。

102學測數學多選10詳解，如附件檔案，請大家指教

以橢圓一焦點F1為圓心做一圓，

  此圓跟橢圓的交點個數只有三種可能：0，1，2

   不可能3個、4個交點

    故可以推測以焦點F1為中心的正方形和橢圓交點個數只有三種可能

    0，1，2

請方家指正益進
謝謝

連高中補習班的俞老師都加入這個大家庭，相信這個討論區內容一定會越來越豐富!!

想請教20,27,30題  謝謝