第一題:
a=231 b=log231
b=log231 c=
c=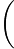 31
31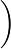 51
51


見圖,可得
a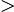 c
c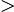 b
b
第二題:3條棉線段,共有6個線頭,今任選其中4個線頭,將兩個線頭打結,共打2個結,則3條棉線段能連成一條的機率?
分母=
C46 2!C24C22
2!C24C22
→六個線頭任取四個,分成兩個兩個一組,共兩組,同一組就綁在一起。看總共有多少種情況。
分子=
C23C12C122!
→三條線段中的某一條線段的兩頭都要被選到(被選到的線頭稱:a,b),另外兩個線段各選一端(被選到的線頭稱:c,d),
(a,b) 與 (c,d) 搭配的情況恰有兩種【ac配,bd配】或【ad配,bc配】可以連成一線。
所求=
C46 2!C24C22C23C12C122!=815
2!C24C22C23C12C122!=815