我們說這種題目,答案會有兩個,因為在平面兩邊均可造成60度
但現在居然解出的情況是重根,那麼另外那個平面呢??如何表示??....消失了嗎??
以上是我的問題~~請各位協助幫忙!!謝謝
平面
E1:
x−y+2z=7與
E2:
x+ky−z=1的夾角之一為
60
,求
k=?
[解答]
E1的法向量為
(1 −1
−1 2)
2),
E2的法向量為
(1 k
k −1)
−1)
 6
6
 k2+2(1
k2+2(1 −1
−1 2)
2) (1
(1 k
k −1)=
−1)=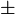 cos60
cos60 =
=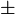 21
21 ⇒
k2−4k+4=0 ⇒
(k−2)2=0 ⇒
k=2