第 17 題
題目:將
8 件不同的物品全部分給甲、乙、丙三人,若其中一人至少得
1 件,一人至少得
2 件,另一人至少得
3 件,則分法有
N 種。將相同的蘋果
4 個及相同的梨子
6 個,全部分給丁、戊、己三人,若每人至少得
1 個(不論是蘋果或梨子),則分法有
M 種。求
N+M 之值=_______。
解答:
N=n(每人至少得一件)−n(某兩人各得一件,第三人獨得六件)
=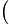 38−C13
38−C13 28+C23
28+C23 1
1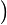 −
−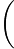 C13
C13 8!1!1!6!
8!1!1!6!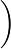 =5628
=5628 M=H43H63−C13H42H62+C23H41H61
M=H43H63−C13H42H62+C23H41H61
(↑ 這是排容原理)
=318
第 21 題
題目:若坐標平面上有一橢圓與
x 軸相切,且其焦點為
F1(2,1) 與
F2(6,2),則此橢圓的短軸長為_______。
解答:
F1F2= 17=2c
17=2c
將
F1 對稱
x 軸得
F 1(2
1(2 −1)
−1),
F 1F2=5=2a
1F2=5=2a
(↑ 畫張圖來看看,想想光學性質就知道了)
 2b=
2b=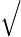
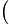 2a
2a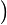 2−
2−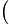 2c
2c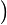 2=2
2=2 2
2
第 27 題
題目:設甲箱內有
2 白球,乙箱內有
3 紅球,現在每次各自箱中隨機取一個球交換,若經過長期達穩定狀態後,求有
2 紅球在甲箱內的機率=_______。(最簡分數)
解答:
轉移矩陣
A=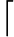
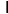
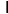
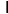
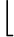 01061213103231
01061213103231






其中上方由左至右分別表示的狀態是甲箱中有兩白、一白一紅、兩紅
轉移成左方的狀態由上而下分別是是甲箱中有兩白、一白一紅、兩紅
(↑ 矩陣裏面的數字要自己算一下喔~算起來很快的!)
再由
A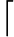
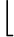 xyx
xyx
 =
=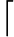
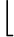 xyx
xyx

且
x+y+z=1,
可解得
x=110 y=53
y=53 z=310
z=310