數學圖形素描教室:用旋轉曲面、多面體、拓樸形狀來創作!結合數學與美學的全新領域
数学デッサン教室 描いて楽しむ数学のかたち
作者: 瑞慶山 香佳
譯者: 陳朕疆
出版社:台灣東販
出版日期:2019/10/28
節錄書中蘋果曲面參數式
◎蘋果曲面的製作方法
該怎麼建構出蘋果曲面呢?讓我們來看看製作方法吧。
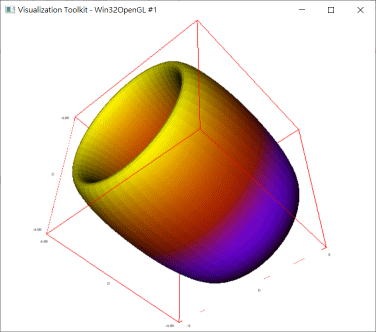
①建構出一個環面。
\(\cases{x=(4+cos u)cos v \cr y=(4+cos u)sin v \cr z=5 sin u},-\pi \le u \le \pi,0 \le v \le 2 \pi\)
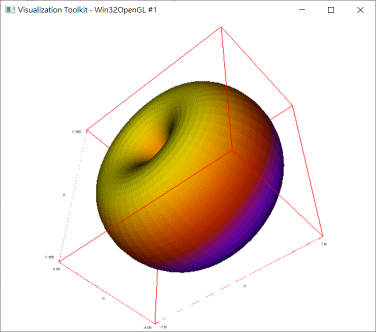
②調整成接近角狀環面的形狀。
\(\cases{x=(4+3.8cos u)cos v \cr y=(4+3.8 cos u)sin v \cr z=5sin u},-\pi \le u \le \pi,0\le v \le 2 \pi\)
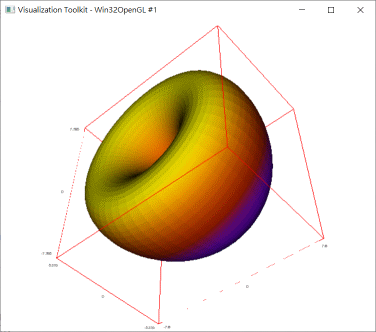
③調整成上方較胖,下方較瘦的形狀。
\(\cases{x=(4+3.8 cos u)cos v \cr y=(4+3.8 cos u)sin v \cr z=5sin u+2 cos u},-\pi \le u \le \pi,0\le v \le 2\pi\)
④建構出蘋果的芯。
\(\cases{x=(4+3.8 cos u)cos v \cr y=(4+3.8 cos u)sin v \cr z=-5log_{10}(1-0.315u)+5sin u+2 cos u},-\pi \le u \le \pi,0\le v \le 2\pi\)
以前要先載入draw.lisp才能使用draw3d指令
但現在draw3d已經是maxima內建指令不再需要先載入draw.lisp
(%i1) load("draw");
(%o1) C:/maxima-5.43.0/share/maxima/5.43.0/share/draw/draw.lisp
以vtk當作渲染器
(%i2) draw_renderer: 'vtk;
(%o2) vtk
①建構出一個環面
(%i6)
x: (4+cos(u))*cos(v);
y: (4+cos(u))*sin(v);
z:5*sin(u);
draw3d(enhanced3d=true,
parametric_surface(x,y,z,u,-%pi,%pi,v,0,2*%pi));
(x) \((cos(u)+4)cos(v)\)
(y) \((cos(u)+4)sin(v)\)
(z) \(5sin(u)\)
(%o6) done
 ②調整成接近角狀環面的形狀
(%i10)
x: (4+3.8*cos(u))*cos(v);
②調整成接近角狀環面的形狀
(%i10)
x: (4+3.8*cos(u))*cos(v);
y: (4+3.8*cos(u))*sin(v);
z:5*sin(u);
draw3d(enhanced3d=true,
parametric_surface(x,y,z,u,-%pi,%pi,v,0,2*%pi));
(x) \((3.8cos(u)+4)cos(v)\)
(y) \((3.8cos(u)+4)sin(v)\)
(z) \(5sin(u)\)
(%o10) done
 ③調整成上方較胖,下方較瘦的形狀
(%i14)
x: (4+3.8*cos(u))*cos(v);
③調整成上方較胖,下方較瘦的形狀
(%i14)
x: (4+3.8*cos(u))*cos(v);
y: (4+3.8*cos(u))*sin(v);
z:5*sin(u)+2*cos(u);
draw3d(enhanced3d=true,
parametric_surface(x,y,z,u,-%pi,%pi,v,0,2*%pi));
(x) \((3.8cos(u)+4)cos(v)\)
(y) \((3.8cos(u)+4)sin(v)\)
(z) \(5sin(u)+2cos(u)\)
(%o14) done
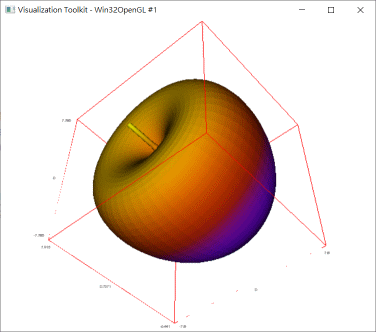
 ④建構出蘋果的芯
(%i18)
x: (4+3.8*cos(u))*cos(v);
④建構出蘋果的芯
(%i18)
x: (4+3.8*cos(u))*cos(v);
y: (4+3.8*cos(u))*sin(v);
z:-5*log(1-0.315*u)/log(10)+5*sin(u)+2*cos(u);
draw3d(enhanced3d=true,
parametric_surface(x,y,z,u,-%pi,%pi,v,0,2*%pi));
(x) \((3.8cos(u)+4)cos(v)\)
(y) \((3.8cos(u)+4)sin(v)\)
(z) \(\displaystyle 5sin(u)+2cos(u)-\frac{5log(1-0.315u)}{log(10)}\)
(%o18) done