如果中間那條是角平分線的話....
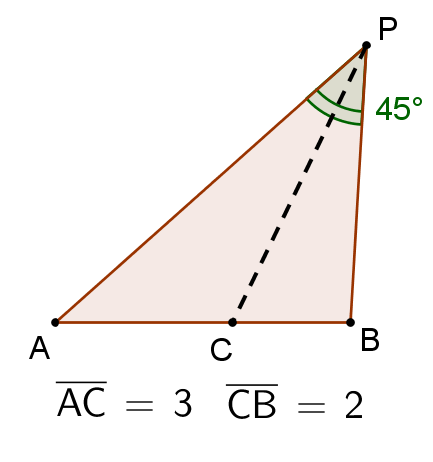
題目:如圖,在 \(\triangle APB\) 中,已知 \(\angle APB=45^\circ\),\(\overline{AC}=3, \overline{CB}=2\),\(\overline{PC}\) 平分 \(\angle APB\),求 \(\triangle APB\) 面積之值。

解答:
因為 \(\overline{PC}\) 平分 \(\angle APB\),所以 \(\overline{AP}:\overline{BP}=\overline{AC}:\overline{CB}=3:2\)
令 \(\overline{AP}=3x, \overline{BP}=2x\) ,其中 \(t\in\mathbb{R^+}\)
在 在 \(\triangle APB\) 中,由餘弦定理,可得 \(5^2=\left(3x\right)^2+\left(2x\right)^2-2\cdot\left(3x\right)\left(2x\right)\cos45^\circ\)
\(\displaystyle \Rightarrow x^2=\frac{25\left(13+6\sqrt{2}\right)}{97}\)
\(\displaystyle \triangle APB \mbox{ 面積 }=\frac{1}{2}\cdot 3x\cdot 2x\cdot \sin45^\circ=\frac{75\left(12+13\sqrt{2}\right)}{194}\)