第 6 題
設
A為二階方陣,
I為二階單位方陣,
AT為
A的轉置矩陣。已知
ATA=AAT=I且
detA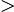 0
0,
A 34
34 =
= 43
43
,則矩陣
A可將直線
x+y=7對應到的圖形方程式為
。
[解答]
矩陣 A 把 點(3,4) 變換到 點(4,3),detA > 0,(A^T)A = A(A^T) = I
可知 A 是旋轉矩陣
利用和角公式可求出
A =
[24/25 7/25]
[-7/25 24/25]
點(3,4) 和 點(4,3) 在 x + y = 7 上
矩陣 A 把 點(3,4) 變換到 點(4,3)
矩陣 A 把 點(4,3) 變換到 點(117/25,44/25)
利用點斜式可求出 31x + 17y = 175
第 7 題
在空間坐標系中,已知
\overline{AB}的中點為
(2,3,4),且
\overline{AB}=10,若動點
P滿足
\vec{PA}\cdot \vec{PB}=1,且
P點到直線
L:
\displaystyle \frac{x-8}{2}=\frac{y-9}{1}=\frac{z-10}{-2}的最短距離為
。
[解答]
向量 PA˙向量 PB = PA * PB * cosθ = 1
由餘弦定理 PA^2 + PB^2 - 2 * PA * PB * cosθ = AB^2
PA^2 + PB^2 = 102
P(x,y,z)、A(2 + a,3 + b,4 + c)、B(2 - a,3 - b,4 - c)
AB^2 = 4a^2 + 4b^2 + 4c^2 = 100, a^2 + b^2 + c^2 = 25
PA^2 + PB^2 = (x - 2 - a)^2 + (y - 3 - b)^2 + (z - 4 - c)^2 + (x - 2 + a)^2 + (y - 3 + b)^2 + (z - 4 + c)^2 = 102
(x - 2)^2 + (y - 3)^2 + (z - 4)^2 = (√26)^2
(2,3,4) 到直線 L:(x - 8)/2 = (y - 9)/1 = (z - 10)/(-2) 的最短距離 = 2√26
所求 = 2√26 - √26 = √26