2.
在底面半徑為6的圓柱內,有兩個半徑也為6的球面,其球心相距20。若作一平面與這兩球面相切,且與圓柱體相交成一橢圓,則此橢圓的長軸為
。
[解答]
長軸長等於球心距
在底面半徑為6的圓柱內,有兩個半徑也為6的球面,其球心距為13。今有一平面與這兩球面相切,且與圓柱面相交成一橢圓,則這個橢圓的長軸與短軸長之和為
。
(99中正高中,
https://math.pro/db/viewthread.php?tid=981&page=3#pid4693)
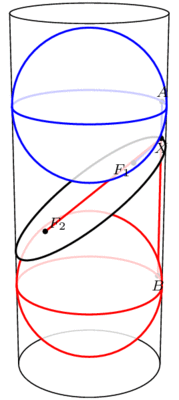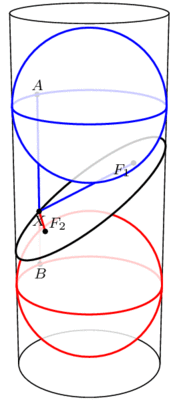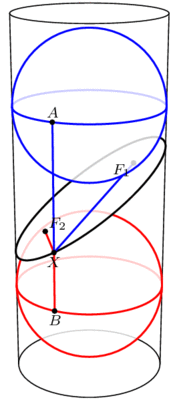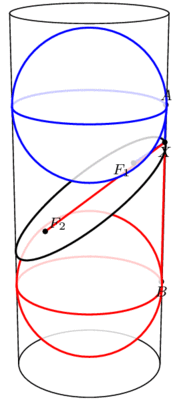
3.
某班有10位學生,投票表達其較喜歡英文老師或數學老師,每人一票且必須投給一位老師,不能兩位老師都選或都不選。開票時,逐一開票。假設,每位學生投給老師的機率均為\( \displaystyle \frac{1}{2} \)。請問,在數學老師的總得票數為6票之條件下,數學老師的得票數在開票過程中,一路領先於英文老師的得票數之機率為
?
[公式]
\( \displaystyle \frac{6-4}{6+4}=\frac{1}{5} \)
13.
求兩圓柱體\( x^2+y^2 \le 1 \)與\( x^2+z^2 \le 1 \)所共有部份體積是
。
求計算\( x^2+y^2\le 1 \),\( y^2+z^2\le 1 \)之共同部分體積
(98彰化女中,
https://math.pro/db/viewthread.php?tid=741&page=1#pid1312)
 GGB檔下載
GGB檔下載
計算1.
\( \Delta ABC \)中,設\( \overline{BC} \),\( \overline{AC} \),\( \overline{AB} \)邊上的高分別為\( h_a \),\( h_b \),\( h_c \),內接圓半徑為r。試證:\( h_a+h_b+h_c \ge 9 r \)
[證明]
\( \displaystyle \Delta=\frac{1}{2} \cdot a \cdot h_a=\frac{1}{2} \cdot (a+b+c) \cdot r \),得\( \displaystyle h_a=\frac{a+b+c}{a}r \)
同理\( \displaystyle h_b=\frac{a+b+c}{b}r \),\( \displaystyle h_c=\frac{a+b+c}{c}r \)
\( \displaystyle h_a+h_b+h_c=r(a+b+c) \left( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right) \ge 9 r \)