如果
f(x)=px+q,對於任意實數
x 及實數
p q
q,我們稱函數
f 是線性的。
如果
F(x+y)=F(x)+F(y) 且
F(ax)=aF(x),對於任意實數
x y
y 及實數
a,我們稱
F 變換是線性的。
下列何者正確?
(A )定義在實數系中的線性變換是線性函數
(B )定義在實數系中的線性函數是線性變換
(C )定義在實數系中的線性函數與線性變換是相同的
(D )在實數系上,線性函數與線性變換並沒有關係
解答:
因為
f(0+0)=f(0)+f(0)
所以
f(0)=0
故對於實數
b =0
=0 的線性函數
f(x)=ax+b 而言,並非線性變換.
接下來繼續證明:如果
f(x) 是定義在實數系上的線性變換,則
y=f(x) 線性函數.
對於任意相異的實數
x1 x2
x2
令
y1=f(x1) y2=f(x2)
y2=f(x2)
則
y1−y2=f(x1)−f(x2)=f(x1−x2)
 x1−x2y1−y2=x1−x2f
x1−x2y1−y2=x1−x2f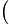 x1−x2
x1−x2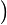 =f
=f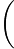 x1−x2x1−x2
x1−x2x1−x2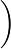 =f(1)為定值
=f(1)為定值
令
f(1)=a 則
且因為線性變換滿足
f(0)=0
所以
y1−0=a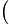 x1−0
x1−0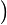
可得
y1=ax1
故
f(x1)=y1=ax1
亦即
f(x)=ax 為線性函數,其中
a=f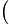 1
1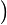
為定值.