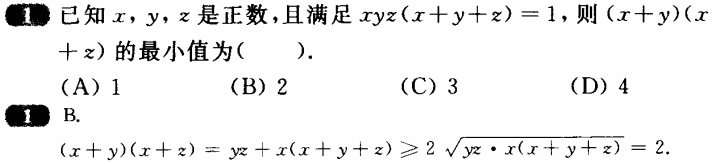1.
化簡\( \displaystyle \frac{1}{sin 10^o}-4sin70^o \)
(奧數教程 高一卷 第11講三角恆等變形)
5.
設\( a_n=7^n+8^n+9^n \),其中\( n=1,2,3,... \),試求\( a_{100} \)除以512的餘數為?
設\( a_n=7^n+8^n+9^n \),其中\( n=1,2,3,... \),試求\( a_{99} \)除以729的餘數為?
(98高中數學能力競賽 台北市筆試一試題)
https://math.pro/temp/hs_math_98.rar
13.
已知\( x,y,z \)為正實數,且滿足\( xyz(x+y+z)=8 \),則\( (x+z)(y+z) \)的最小值為?
若三正數\( x,y,z \)滿足\( xyz(x+y+z)=25 \),則\( (x+y)(y+z) \)的最小值為?
(97高中數學能力競賽第四區筆試二)
https://math.pro/db/viewthread.php?tid=919
已知\( x,y,z \)是正数,且满足\( xyz(x+y+z)=1 \),则\( (x+y)(x+z) \)的最小值为?
(新奧數教程高二卷第2講 平均不等式和科西不等式,高中數學101 P353)