已知在一個與變化量
x、
y有關的線性規劃作業中,有三個限制條件。在坐標平面上畫出符合這三個限制條件的區域,最後得到的可行解區域是一個三角形
ABC及其內部區域(包含邊界),已知
A(3 3)
3),
B(5 −7)
−7),
C(

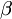 )
)。在此可行解區域中,當目標函數為
f(x y)=x+2y
y)=x+2y時,得到在
A點有最大值,在
B點有最小值。現因環境條件改變的需要,加入了第四個限制條件
ax+by c
c,結果符合所有限制條件的可行解區域變成一個四邊形區域,頂點少了
A(3 3)
3),但新增了頂點
D(1 1)
1),
E(4 −2)
−2)。若已知滿足上述條件的
C(

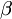 )
),其中

可能的最小範圍為
m

 n
n,
m、
n為整數。請問數對
(m n)=
n)=?
請問 四 2.