105模擬考

第1題也有完全不坐標化的方法 (正餘弦定理 & 旋轉)

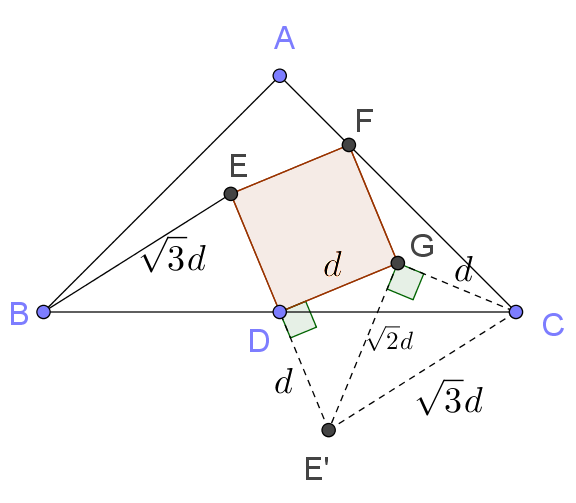
假設 \(\overline{DG}=d\)，則 \(\overline{DF}=\sqrt{2}d\)
在\(\triangle DCF\)中，由正弦定理可知 \(\frac{\sqrt{2}d}{\sin{45^{\circ}}}=2R\)，\(R=d\)
又因為 \(G\) 在 \(\triangle DCF\) 內部，故 \(G\) 就是 \(\triangle DCF\)之外心，\(\overline{GC}=d\)

再將 \(\triangle DEB\) 以 \(D\) 為中心逆時針旋轉 \(180^{\circ}\)，
使得 \(B\) 與 \(C\) 重合，\(E\) 變成 \(E’\)
則 \(\triangle E’CG\) 的三邊長正好是直角三角形的三邊長 \(\sqrt{3}d,d,\sqrt{2}d\)
因此 \(\angle CGE’=90^{\circ}\)，而 \(\angle CGD=90^{\circ}+45^{\circ}=135^{\circ}\)
最後在 \(\triangle DCG\) 中使用餘弦定理就解出 \(d\) 了!

\(\overline{CD}^2=d^2+d^2-2dd\cos{135^{\circ}}\)

\(2^2=2d^2+\sqrt{2}d^2\)

\(d^2=\frac{4}{2+\sqrt{2}}=4-2\sqrt{2}\)