|
|
1#
大 中
小 發表於 2015-1-16 20:46 只看該作者
請教兩題(角平分線,與乘法公式)
請教兩題,如附件,謝謝!!
(1)
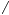 B=60 B=60 , 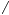 A A 與 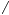 C C 的角平分線交於 I,若 AE=p BE=q BE=q BD=r BD=r CD=s CD=s, 求 AC 的長度? (用 p q q r r s s 表示)


答案: p+s
(2)
若 (x+ x2+2014)(y+ x2+2014)(y+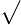 y2+2104)=2014 y2+2104)=2014 ,求 2x2−5xy−7y2−9x−9y+543= ?
答案: 543
附件
-
 0116-2.rar
(48.8 KB)
0116-2.rar
(48.8 KB)
-
2015-1-16 20:46, 下載次數: 6155
|