Consider the recurrence relation for Fibonacci numbers
F(n)=F(n−1)+F(n−2). Without solving this recurrence, compare
F(n) to
G(n) defined by the recurrence
G(n)=G(n−1)+G(n−2)+1. It seems obvious that
G(n)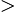 F(n)
F(n)(because of the extra 1). Yet the following is a seemingly valid proof(by induction) that
G(n)=F(n)−1. We assume, by induction, that
G(k)=F(k)−1 for all
k such that
1 k
k n
n, and we consider
G(n+1):
G(n+1)=G(n)+G(n−1)+1=F(n)−1+F(n−1)−1+1=F(n+1)−1
What is wrong with this proof?
請各位老師幫忙 謝謝
(看不出哪裡有錯誤)