題目分配總數：一. 單選題 10 題 二. 填充題 15 題 三.計算題 1 題 (1)(2) 小題
填充15題

pic.png (34.35 KB)

2012-4-7 22:28

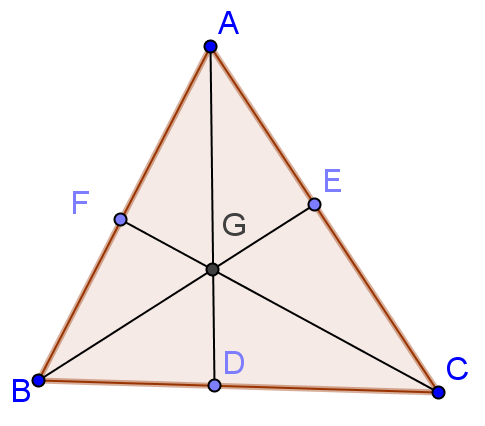
如圖，滿足 \( \frac{\overline{AG}}{\overline{GD}} + \frac{\overline{BG}}{\overline{GE}} + \frac{\overline{CG}}{\overline{GF}} =2012 \)

求  \( \frac{\overline{AG}}{\overline{GD}} \cdot \frac{\overline{BG}}{\overline{GE}} \cdot \frac{\overline{CG}}{\overline{GF}} \)

編號的字母可能不太一樣

填充 1x

\( a,\, b>0\) (印象中)

\(A=\sqrt{a^{2}+b^{2}-\sqrt{2}ab}\), \(B=\sqrt{49+a^{2}-7\sqrt{20}}\), \(C=\sqrt{64+b^{2}-8\cdot\sqrt{3}}b\)求 \(A+B+C\) 的最小值。

註：猜測題目的 \(C\) 打錯了，裡面應該有 \(a\)，改成 \(\sqrt{49+a^{2}-7\cdot\sqrt{2}a}\) 可能是原本正確的題意。

填充 1x
\( f(x)=(1+x+x^{2}+x^{3}+x^{4})^{11}=a_{0}+a_{1}x+a_{2}x^{2}+\ldots+a_{44}x^{44}\)，求 \(a_{6}\)。

填充 x (超眼熟的題目，考前一天做100基隆高中，才做到)

\( f(x) \) 是一個 98 次多項式，且滿足 \( f(n) =\frac{1}{n}\), \( n=1,2,3,\ldots, 99 \)，求 \( f(100) \)

手殘，打錯，已修正，感謝！

遞迴不難做，

但要注意第八項為 0，遞迴關係為 \( a_{n+3} =a_{n+1}+a_n \)

從 1-12 分別為 0,1,1,1,2,2,3,0,5,3,5,8

之後再做 13-20 0,1,1,1,2,2,3,4

其實和  1-12 一樣

所以答案是 \( 8 \times 4 =32 \)

但是我也眼殘，沒看到 20 ，印象中我只算到 12階

回程的路上，想到，這題其實可以用立方和加三倍角公式做，如下

\(\displaystyle \cos^{2}10^{\circ}+\cos^{2}50-\cos50^{\circ}\cos10^{\circ}=\frac{\cos^{3}10^{\circ}+\cos^{3}50^{\circ}}{\cos10^{\circ}+\cos50^{\circ}}\)
\(\displaystyle=\frac{1}{4}\cdot\frac{4\cos^{3}10^{\circ}+4\cos^{3}50^{\circ}}{\cos10^{\circ}+\cos50^{\circ}}\)
\(\displaystyle=\frac{1}{4}\frac{4\cos30^{\circ}+4\cos150^{\circ}+3(\cos10^{\circ}+\cos50^{\circ})}{\cos10^{\circ}+\cos50^{\circ}}\)
\(\displaystyle=\frac{3}{4}\)

實在厲害...
來補上自己的考試中未竟之功...考試中一直在想特殊化，用特例帶數字，但一直想正三角。

但其實直角三角形才會好算。

特例：令 \( A(0,0), B(2,0), C(0,2), D(1,1), G(t,t)\)， \( t \) 待決定，以滿足題目條件。

則邊長比積和可表示為 \(\displaystyle \frac{t}{1-t}+\frac{2-t}{t}+\frac{2-t}{t}=2012\)

整理成 \( \Rightarrow t^{2}+2(2-t)(1-t)=2012(1-t)t\Rightarrow2015t^{2}-2018t+4=0\)。

邊長比的積 \(\displaystyle \frac{(2-t)^{2}}{(1-t)t}=\frac{t^{2}-4t+4}{t-t^{2}}\times\frac{2015}{2015} \)

\(\displaystyle =\frac{2018t-4-8060t+8060}{4-3t}=\frac{-6042t+8056}{-3t+4}=2014 \)。

不過這樣的作法，也只能用在填充題上而已，有沒有更漂亮簡單的特例呢？

應該只有給實數而已，因為右式其實是 \( tan \) 五倍角

另外 \( f(x)=(1+x+x^{2}+x^{3}+x^{4})^{11} \) 這題，剛才想到一個美妙的辦法

補項，把 \( x^{5}+x^{6}+\ldots \) 補到括號裡。

那麼新的函數就是  \( \displaystyle\frac{1}{(1-x)^{11}}\)，以微分計算 \( x^{6} \) 係數

\(\displaystyle\frac{1}{6!}\frac{d^{6}}{dx^{6}}\frac{1}{(1-x)^{11}}=\frac{C_{6}^{16}}{(1-x)^{17}}=8008\frac{1}{(1-x)^{17}}\Rightarrow8008 \)

但補了之後，展開中會多出 \( x\cdot x^{5} \) 和 \( 1\cdot x^{6}\) 即 \(\displaystyle\frac{11!}{10!1!}+\frac{11!}{1!1!9!}=11+110=121\)

所以答案就是 \( 8008-121=7887\)。

• 
  

  AAADEF 三A相鄰有 \(4!\) 種排法

AAADBEBF \(C_{2}^{5}\times1\)

AAADEFBB \(5\times0\)

AABADEFB \((2\cdot5)\times8\)

ABABADEF \(C_{2}^{2}\times C_{2}^{9}\)

AABBADEF \(2\times C_{2}^{2}\)

以上 \( \times \) 前方代表 2B 的插入方法數，後方則是2B插入後2C再插入的方法數

故此類有 AAADEF \(4!\times(10+80+36+2)=3072\)

• AADEFA 2A相鄰但3A不相鄰 \(3!\cdot4\cdot3\)

AADEFBAB \(C_{2}^{6}\times8\)

AADEFABB \(6\times C_{2}^{2}\)

ABADEFAB \(6\times C_{2}^{9}\)

ABBADEFA \(1\times8\)

故此類有 \( (3!\cdot4\cdot3)\times(120+6+216+8)=25200 \)

• ADAEAF \(3!\cdot C_{3}^{4}\)

ADAEAFBB \(7\times8\)

ADAEABFB \(C_{2}^{7}\times C_{2}^{9}\)

故此類有 \((3!\cdot C_{3}^{4})\times(56+21\cdot36)=19488\)

綜合以上三類共有 \(3072+25200+19488=47760 \)

以上做完，其實比取捨原理的麻煩多了