計算題第 1 題:
三角形ABC,∠A的內角平分線\( \overline{AT} \)交\( \overline{BC} \)於T點,試證\( \overline{AT}=\sqrt{\overline{AB}\cdot \overline{AC}-\overline{BT}\cdot \overline{CT}} \)
[解答]
由三角形的內角平分線的內分比性質,
可得 \(\overline{AB}:\overline{AC}=\overline{BT}:\overline{CT}\)
因此可令 \(\overline{AB}=x, \overline{AC}=y, \overline{BT}=kx, \overline{CT}=ky\),其中 \(k\) 為正實數,
則題意等同於要求證: \(\overline{AT}^2=xy-k^2xy\)
因為 \(\cos ∠ATB = \cos(180^\circ - ∠ATC)\)
所以 \(\cos ∠ATB = -\cos(∠ATC)\)
在 \(\triangle ABT\) 與 \(\triangle ACT\) 中,由餘弦定理可得
\(\displaystyle \cos ∠ATB=\frac{\overline{AT}^2+(kx)^2-x^2}{2\overline{AT}\times kx}\)
\(\displaystyle \cos∠ATC= \frac{\overline{AT}^2+(ky)^2-y^2}{2\overline{AT}\times ky}\)
因此 \(\displaystyle \frac{\overline{AT}^2+(kx)^2-x^2}{2\overline{AT}\times kx}=-\frac{\overline{AT}^2+(ky)^2-y^2}{2\overline{AT}\times ky}\)
即可解得 \(AT^2 = xy-k^2xy.\)
註:1. 可是這樣一點也不豪華耶~XDD
那補充一個 Stewart's theorem 好了~
Stewart's theorem:
http://en.wikipedia.org/wiki/Stewart's_theorem
也是用餘弦定理算兩次就可以證出來的定理。
2. 有些朋友可能對內分比性質不熟悉,簡單證明如下:
a. 自 \(T\) 往 \(\overline{AB},\overline{AC}\) 作垂線,

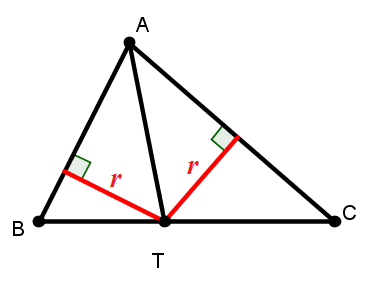
如圖,可得 \(\triangle ABT : \triangle ACT = \frac{1}{2}\cdot \overline{AB}\cdot r : \frac{1}{2}\cdot \overline{AC}\cdot r=\overline{AB}:\overline{AC}\)
b. 自 \(A\) 往 \(BC\) 直線作垂線,

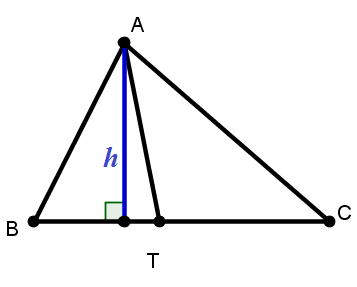
如圖,可得 \(\triangle ABT : \triangle ACT = \frac{1}{2}\cdot \overline{BT}\cdot h : \frac{1}{2}\cdot \overline{CT}\cdot h=\overline{BT}:\overline{CT}\)
由 a. b. 可得 \(\overline{AB}:\overline{AC} =\overline{BT}:\overline{CT}.\)