回復 51# c90378 的帖子
第7題
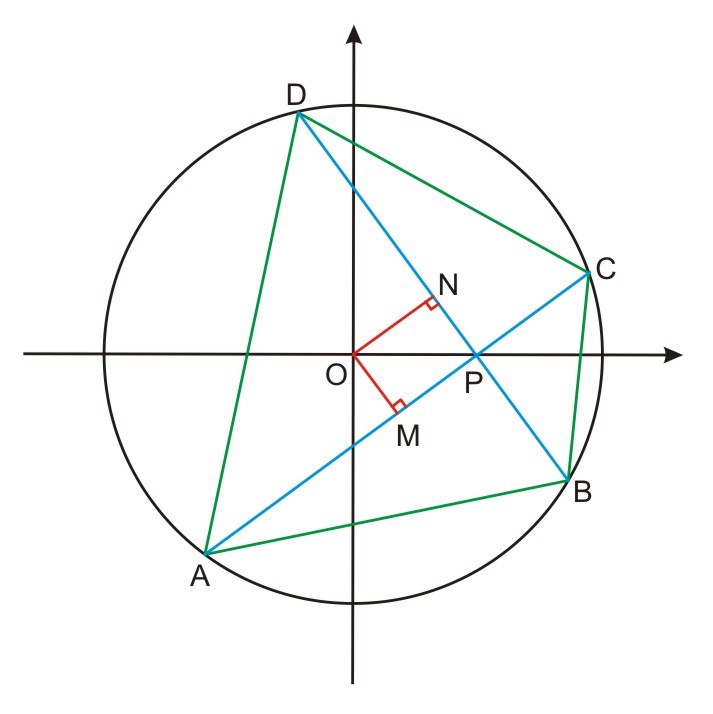
設圓\(O\):\(x^2+y^2=4\),四邊形\(ABCD\)為圓\(O\)的內接四邊形,已知\(\overline{AC}\)與\(\overline{BD}\)互相垂直交於\((1,0)\),則四邊形\(ABCD\)面積的最大值為 。
[解答]
\(\begin{align}
& P\left( 1,0 \right)\ ,\ \overline{OA}=\overline{OB}=2\ ,\ \overline{OM}=a\ ,\ \overline{ON}=b \\
& \overline{AC}=2\sqrt{4-{{a}^{2}}}\ ,\ \overline{BD}=2\sqrt{4-{{b}^{2}}} \\
& {{a}^{2}}+{{b}^{2}}=1 \\
& ABCD=\frac{1}{2}\times \overline{AC}\times \overline{BD}=2\times \sqrt{4-{{a}^{2}}}\times \sqrt{4-{{b}^{2}}}\le 4-{{a}^{2}}+4-{{b}^{2}}=7 \\
\end{align}\)
附件
-
 20180809.jpg
(52.43 KB)
20180809.jpg
(52.43 KB)
-
2018-8-9 11:29