回覆 20# JJM 的帖子
6 個關卡(k = 6),從某 1 關先闖,共闖 7 關,即換關(移動) 6 次(n = 6) 後回到初始關由於可從任一關先闖,故公式中的 1/k 要拿掉
[[i] 本帖最後由 thepiano 於 2024-4-2 00:01 編輯 [/i]] 想請問J 和 R 謝謝
-------------
打錯了 是J和M 才對(R前面有了)
[[i] 本帖最後由 g112 於 2024-4-2 11:50 編輯 [/i]]
回覆 22# g112 的帖子
第 J 題對邊長度兩兩相同的四面體(等腰四面體),其六個兩面角的餘弦值之和 = 2
所求 = 2[2 - (-1/2)] = 5 [quote]原帖由 [i]thepiano[/i] 於 2024-4-2 10:37 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=25644&ptid=3823][img]https://math.pro/db/images/common/back.gif[/img][/url]
第 J 題
對邊長度兩兩相同的四面體(等腰四面體),其六個兩面角的餘弦值之和 = 2
所求 = 2[2 - (-1/2)] = 5 [/quote]
謝謝鋼琴老師,另外想問這性質有相關文獻嗎
剛google了一下找不太到他的證明,謝謝
回覆 24# g112 的帖子
可以參考這篇「四面體的餘弦定理」,但是這篇所討論的正四面體更為廣義一些。 (運用當中的定理四可以處理這一題)[url]https://web.math.sinica.edu.tw/mathmedia/HTMLarticle18.jsp?mID=40106[/url]
[[i] 本帖最後由 小超人Mo 於 2024-4-2 11:53 編輯 [/i]]
回覆 24# g112 的帖子
等腰四面體內接於一長方體,建立空間座標系設六個兩面角分別是 α、α、β、β、γ、γ
利用兩平面的夾角 = 其法向量夾角的補角,可求出 cosα,而 cosβ 和 cosγ 同理
可證出 cosα + cosβ + cosγ = 1
回覆 22# g112 的帖子
第 M 題ω = t(-√3 + 4i) + (2 - 2t)i = -√3t + (2t + 2)i
在複數平面上,ω 的圖形是直線 2x + √3y = 2√3
z^8 = -1/2 + (√3/2)i 的 8 次方根 = cos[(3k + 1)π/12] + isin[(3k + 1)π/12]
在複數平面上,z 所形成的 8 個點在單位圓上
畫圖可知當 k = 1 時,z = 1/2 + (√3/2)i,點 z(1/2,√3/2) 到直線 2x + √3y = 2√3 有最小距離 (4√21 - 5√7)/14
[[i] 本帖最後由 thepiano 於 2024-4-2 12:45 編輯 [/i]] 好的 謝謝兩位老師
回覆 21# thepiano 的帖子
懂了!謝謝鋼琴老師! [quote]原帖由 [i]yymath[/i] 於 2024-4-1 19:58 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=25633&ptid=3823][img]https://math.pro/db/images/common/back.gif[/img][/url]公式講解影片 給你參考
影片上集
[url]https://youtu.be/AVh4ZSws6Xk?si=pvtbOBnX_W6X68F0[/url]
下集
[url]https://youtu.be/uqsj31bc1AY?si=f_4j-J88Q0s2bJw-[/url] [/quote]
請問[url]https://chu246.blogspot.com/2022/07/1112.html[/url],
111年台南女中第2次教甄的第15題,青蛙,可以用這題的公式修改嗎?
或是有沒有快方法?謝謝。 不好意思,想請教一下 第K題
回覆 31# std310185 的帖子
當
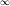 (
( 5x5+3x4+4x3+3x−
5x5+3x4+4x3+3x− 3x3+3x2+4x+1)
3x3+3x2+4x+1) 
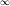 (
( 5x5+3x4−
5x5+3x4− 3x3+3x2)
3x3+3x2) 
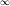 (x
(x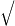 51+x3−x
51+x3−x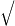 31+x3)
31+x3) 
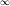 (x(1+35x)−x(1+33x))=−52
(x(1+35x)−x(1+33x))=−52[[i] 本帖最後由 Jimmy92888 於 2024-4-4 05:50 編輯 [/i]]
回覆 32# Jimmy92888 的帖子
原來如此,謝謝Jimmy老師 試著整理手寫解答 有一些算不出來 參考了老師們的寫法才整理完成~[url]https://drive.google.com/file/d/1RgvG261Yu1Z4vmA1w1b_gGwEJCDhnnEK/view?usp=drivesdk[/url] 想請教L有沒有不需要微分方程的作法?謝謝!
回覆 35# JJM 的帖子
第L題注意f(x)的次數
回覆 36# peter0210 的帖子
懂了 謝謝老師!頁:
1
[2]