2020TRML
因新冠肺炎,今年賽制有所改變僅團體賽、思考賽、個人賽
題目如附件,供各位老師參考
回復 1# superlori 的帖子
太久沒來Math Pro不但密碼忘了
連照片也不會貼了
有詢問主辦單位九九文教,下週才會公佈答案
在此先po個簡答,拋磚引玉
如有錯誤,麻煩提出
參考詳解得等我學會如何po照片再發XD
2020TRML個人賽
1. 82
2. 3/4
3. 50
4. 12 sqrt(3)
5. 5
6. 28
7. 513
8. 42
9. (-1+sqrt(13))/4
10. 3 sqrt(3)
11. 420
12. 12
2020TRML團體賽
1. 3 sqrt(3) -9/2
2. sqrt(35)/5
3. sqrt(35)/70
4. sqrt(13) pi /2
5. 80 + 24 sqrt(11)
6. 390
7. 50
8. 6
9. 1365
10. 1/14 只有LibreOffice檔,沒有MS Office Word檔。
2019TRML討論文章[url]https://math.pro/db/thread-3196-1-1.html[/url]
2018TRML討論文章[url]https://math.pro/db/thread-3010-1-1.html[/url]
2017TRML討論文章[url]https://math.pro/db/thread-2854-1-1.html[/url]
2016TRML討論文章[url]https://math.pro/db/thread-2591-1-1.html[/url]
2015TRML討論文章[url]https://math.pro/db/thread-2339-1-1.html[/url]
2014TRML討論文章[url]https://math.pro/db/thread-2028-1-1.html[/url]
2013TRML討論文章[url]https://math.pro/db/thread-1733-1-1.html[/url]
2012TRML討論文章[url]https://math.pro/db/thread-1486-1-9.html[/url]
2011TRML討論文章[url]https://math.pro/db/thread-1247-1-5.html[/url]
2010TRML討論文章[url]https://math.pro/db/thread-1075-1-3.html[/url]
2009TRML討論文章[url]https://math.pro/db/thread-1167-1-1.html[/url]
2007TRML討論文章[url]https://math.pro/db/thread-1483-1-14.html[/url]
2001TRML討論文章[url]https://math.pro/db/thread-1287-1-1.html[/url]
2000TRML討論文章[url]https://math.pro/db/thread-1967-1-1.html[/url]
TRML1999-2007
[url]http://sites.chhs.hcc.edu.tw/shu-xue-tian-de/li-jie-shi-ti-zhuan-qu/tai-wan-qu-gao-zhong-shu-xue-jing-sai-trml-li-jie-shi-ti-1999-2007[/url]
寸絲部落格也有題目和詳解
[url]http://tsusy.wordpress.com/category/%E6%95%B8%E5%AD%B8/trml/[/url]
2013~2015歷屆試題詳解
[url]http://203.72.198.200/sections/3150/pages/7369?locale=zh_tw[/url]
111.4.2補充
若
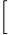 −1−
−1− 3
3 3−1
3−1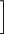 100=
100=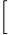 acbd
acbd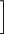
2012TRML團體賽
若
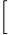 −
− 3−11−
3−11− 3
3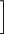 99=
99=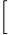 acbd
acbd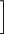
(111樟樹實創高中,[url]https://math.pro/db/thread-3617-1-1.html[/url])
回復 2# Fermat 的帖子
官方版的2020TRML團體賽、個人賽答案已公告順便附上參考詳解
有些題解得很暴力、很勉強、不漂亮
請見諒
應該有更好解法
頁:
[1]