109新竹建功國中部
請教13~15 1.在一邊長為
為
在一邊長為
thepiano解題
(99家齊女中,[url]https://math.pro/db/viewthread.php?tid=958&page=1#pid2184[/url])
2.
若
Joy091解題
(100中壢高中二招,[url]https://math.pro/db/viewthread.php?tid=1170&page=3#pid3975[/url])
8.
若有一枚特製的硬幣,出現反面機率為出現正面機率的兩倍,小明擲此硬幣8次,他從數線上的0開始,若投擲的錢幣出現正面,則向數線的正向走1單位;若出現反面,則向數線的負向走1單位。如果他在移動的過程中曾經達到數線正向4的機率為何[u] [/u]。
小杰投擲一枚公正的錢幣8次,他從數線上的0開始,若投擲的錢幣出現正面,則向數線的正向走1單位;若出現反面,則向數線的負向走1單位。如果他在移動的過程中曾達到數線正向4的機率為
(A)69 (B)151 (C)257 (D)293 (E)313
連結有解答
(2016AMC12,[url]https://math.pro/db/thread-2445-1-1.html[/url])
9.
 2499=
2499= A+
A+ B
B  B
B 1000
1000 2009=
2009= x+
x+ y
y  x
x y
y y)
y) [url]https://math.pro/db/thread-664-1-1.html[/url]
12.
圓
一個半徑為10的圓被兩條互相垂直的直線分成四個部分,面積分別為
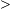 R2
R2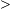 R3
R3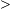 R4
R4(A)40 (B)44 (C)48 (D)52 (E)56
thepiano解題
(103台南一中數理暨語文資優班,[url]https://math.pro/db/viewthread.php?tid=2283&page=1#pid13606[/url])
13.
設
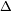 ABC
ABC\Delta ABC中,\overline{CD}交\overline{BE}於F,已知\Delta BDF面積為10,\Delta BCF面積為20,\Delta CEF面積為16,則四邊形區域ADFE之面積為 。
(100苑裡高中,[url]https://math.pro/db/viewthread.php?tid=1178&page=2#pid4270[/url])
19.
將長方形ABCD沿著對角線\overline{AC}摺起,使得平面ABC與平面ADC互相垂直,若\overline{AB}=2,\overline{BC}=1,試求\overline{BD}=[u] [/u]。
[公式]
\displaystyle \sqrt{\frac{a^4+b^4}{a^2+b^2}}
將一塊邊長\overline{AB}=a公分(a>0)、\overline{BC}=b公分(b>0)的長方形鐵片ABCD沿對角線\overline{BD}對摺後豎立,使得平面ABD與平面CBD垂直,則A、C兩點(在空間的距離\overline{AC}=[u] [/u]。
(107松山工農,[url]https://math.pro/db/thread-2972-1-1.html[/url])
20.
正方形ABCD中,\Delta ABF、\Delta CEF及\Delta DAE的面積分別為4、5、6,請問\Delta AEF的面積為何?
計算2.
有一平行四邊形ABCD,若過頂點A作一圓,且分別交\overline{AB}、\overline{AD}及對角線\overline{AC}或其延長線於E點、F點、G點。請利用托勒密定理證明:\overline{AC}\times \overline{AG}=\overline{AB}\times \overline{AE}+\overline{AD}\times \overline{AF}
hua0127解題
[url]https://math.pro/db/thread-1896-1-1.html[/url]
計算4.
實係數方程式x^4+ax^3+bx^2+cx+d=0有四根為\alpha、\beta、\gamma、\omega,其中\alpha+\beta=3+4i且\gamma \omega=5+2i,則a+b+c+d=[u] [/u]。
實係數方程式x^4+ax^3+bx^2+cx+d=0有四根為\alpha、\beta、\gamma、\omega,其中\alpha+\beta=3+6i且\gamma\omega=4+3i,則a+b+c+d=[u] [/u]。
weiye解題
(107建國中學二招,[url]https://math.pro/db/viewthread.php?tid=2970&page=2#pid19057[/url])
已知a,b,c,d為實數,且方程式x^4+ax^3+bx^2+cx+d=0有四個虛根,其中兩根的乘積為13+i,另外兩根的和為3+4i,求 a,b之值?
[url]https://math.pro/temp/qq60.pdf[/url]
回復 2# bugmens 的帖子
感謝老師回復 1# nansir0936 的帖子
第 14 題正方形ABCD,其中\overline{CB}=\overline{CF}、\overline{EG}// \overline{AB}、\overline{EG}=3、\overline{FG}=1,求正方形邊長為何?
參考附圖,答案是 6
回復 4# thepiano 的帖子
跟老師一樣延長了EG,結果就卡關了,平分角BCF才是關鍵啊,謝謝老師指點迷津! 想請教一下填充第4,5,6,11,15,16題話說這份有答案嗎?
想確認一下
可能錯很多,煩請大力指正!
回復 6# abc409212000 的帖子
第8題若有一枚特製的硬幣,出現反面機率為出現正面機率的兩倍,小明擲此硬幣8次,他從數線上的0開始,若投擲的錢幣出現正面,則向數線的正向走1單位;若出現反面,則向數線的負向走1單位。如果他在移動的過程中曾經達到數線正向4的機率為何[u] [/u]。
硬幣不是公正的,答案應是\displaystyle \frac{209}{6561}
第18題
直線L_1經A(1,1,0)、B(2,1,1),直線L_2經C(1,1,1)、D(1,3,2),另一直線L_3過E(2,0,1)且與L_1、L_2均相交,則L_2、L_3之交點坐標為[u] [/u]。
104桃園高中考過,答案應是 (1,-1,0)
其它您寫的答案都是正確的
回復 6# abc409212000 的帖子
第 4 題若a=4sin20^{\circ}+tan20^{\circ}且\displaystyle b=\frac{1}{sin10^{\circ}}-4sin70^{\circ},則\displaystyle \frac{a}{b}=[u] [/u]。
[解答]
分開算,a = √3,b = 2
第 5 題
將任意三位數重複寫兩次構成一個新的六位數,例如:135135、256256…。像這樣的六位數中,能被2821整除的最小數為[u] [/u]。
[解答]
2821 = 7 * 13 * 31
任意三位數重複寫兩次構成的六位數是 1001 = 7 * 11 * 13 的倍數
所以所求 = 1001 * 31 * 4
第 6 題
\Delta ABC中,\overline{CA}=\overline{CB}且∠C=20^{\circ},分別在\overline{AC}、\overline{BC}上取D點、E點,使得∠DAE=10^{\circ}、∠EBD=20^{\circ},請問∠AED的度數為[u] [/u]。
幾何名題,做法 google 一下
第 11 題
二次函數y=ax^2+bx+c的圖形一部分如圖所示,則a值的範圍為[u] [/u]。
[解答]
過 (0,1),c = 1
過 (1,0),a + b + c = 0,b = - a - 1
開口朝下,a < 0,頂點又在第二象限,b < 0
故 -1 < a < 0
回復 7# thepiano 的帖子
感謝thepiano老師,已重新修改為正確答案順手附上第八題修正後過程,供參考
#回覆15題
如圖,在正五邊形ABCDE內取一點F,使得\overline{AF}=\overline{AE}、\overline{FC}⊥ \overline{CD},求∠AFE=[u] [/u]度。淺見提供
回復 6# abc409212000 的帖子
第16題如圖,\Delta ABC中,\overline{CD}、\overline{BE}分別為兩邊上的高且交於F點。若\overline{AB}=7、\overline{BC}=5、\overline{DE}=3,則\overline{BE}的長度為何?[u] [/u]
[解答]
B、C、E、D四點共圓
\begin{align} & \Delta ADE\sim \Delta ACB \\ & \frac{\overline{AE}}{\overline{AB}}=\frac{\overline{DE}}{\overline{CB}} \\ & \frac{\overline{AE}}{7}=\frac{3}{5} \\ & \overline{AE}=\frac{21}{5} \\ & \overline{BE}=\sqrt{{{\overline{AB}}^{2}}-{{\overline{AE}}^{2}}}=\frac{28}{5} \\ \end{align}
不過如此一來,\overline{BE}>\overline{BC},不合,故此題應送分
回復 6# abc409212000 的帖子
參考答案如下:[url]http://www.shiner.idv.tw/teachers/download/file.php?id=3215[/url] 感謝thepaino、王重鈞老師!!
問題皆已解決,附上第六題可參考網站
[url]https://nbhwj.com/2013/10/%E4%B8%80%E9%81%93%E5%87%A0%E4%BD%95%E9%A2%98%E7%9A%84%E5%A4%9A%E7%A7%8D%E8%AF%81%E6%98%8E%E6%96%B9%E6%B3%95/[/url] 想說嘗試看看第六題代數解
接下來卻卡關...
再麻煩各位老師
回覆14#
淺見分享回復 15# 王重鈞 的帖子
真是太感謝您了!回覆16#
不客氣!很少來逛這裡 能幫上忙我也很開心! 計算第一題的想法 還請各位大神檢驗一下是否正確已知f(x)=|\;log x|\;,若0<a<b且f(a)=f(b),其中a,b為實數,證明:a+2b>3。
[解答]
設A(a,-log(a))、B(b,log(b))
由題目條件,可知\displaystyle b=\frac{1}{a},且0<a<1
故\displaystyle a+2b=a+\frac{2}{a} 在0<a<1為遞減函數
可知\displaystyle a+\frac{2}{a}>3
感謝鋼琴老師糾正筆誤
回復 18# satsuki931000 的帖子
A(a,-log(a))填七
設平面上有\Delta ABC與\Delta PQR,若2\vec{PA}+\vec{PB}+\vec{PC}=\vec{BC},\vec{QA}+3\vec{QB}+\vec{QC}=\vec{CA},\vec{RA}+\vec{RB}+4\vec{RC}=\vec{AB},求\Delta PQR與\Delta ABC之面積比值[u] [/u]。[解答]
可能太簡單,乏人問津,小弟自告奮勇。
2\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{BC}
\overrightarrow{QA}+3\overrightarrow{QB}+\overrightarrow{QC}=\overrightarrow{CA}
\overrightarrow{RA}+\overrightarrow{RB}+4\overrightarrow{RC}=\overrightarrow{AB}
2\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{BC}-\overrightarrow{PC}
3\overrightarrow{QB}+\overrightarrow{QC}=\overrightarrow{CA}-\overrightarrow{QA}
\overrightarrow{RA}+4\overrightarrow{RC}=\overrightarrow{AB}-\overrightarrow{RB}
2\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{BP}
3\overrightarrow{QB}+\overrightarrow{QC}=\overrightarrow{CQ}
\overrightarrow{RA}+4\overrightarrow{RC}=\overrightarrow{AR}
\overrightarrow{PA}=\overrightarrow{BP}
3\overrightarrow{QB}=2\overrightarrow{CQ}
2\overrightarrow{RC}=\overrightarrow{AR}
....能找到P在\overline{AB}上,且\overline{AP}:\overline{PB}=1:1
Q在\overline{BC}上,\overline{BQ}:\overline{QC}=2:3
R在\overline{AC}上,\overline{AR}:\overline{RC}=2:1
方能找到\Delta PQR:\Delta ABC的比值了。
頁:
[1]