109大園高中
請問填充第 3 題---
如果試題有誤,可以再留言跟我說
英文試題找得有點辛苦~ [quote]原帖由 [i]Superconan[/i] 於 2020-5-24 23:24 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=21262&ptid=3334][img]https://math.pro/db/images/common/back.gif[/img][/url]
請問填充第 3 題
---
如果試題有誤,可以再留言跟我說
英文試題找得有點辛苦~ [/quote]
#3先給答案 若沒有限制x,y,z屬性
(x,y,z)= (-2/5,-3/7,-1) or (2/5,3/7,1)or (-i,i,i) or (i,-i,i) or (i,i,-i)or (-i,-i,i) or(-i,i,-i)or (i,-i,-i)
回復 1# Superconan 的帖子
填充第3題這題應是求實數解,
 y
y z
z  y
y z
z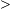 0
0  y=tan2B
y=tan2B z=tan2C
z=tan2C A+B+C=
A+B+C= x+x1=sin2Acos2A+sin2Acos2A=1cos2Asin2A=2sinAy+y1=2sinB
x+x1=sin2Acos2A+sin2Acos2A=1cos2Asin2A=2sinAy+y1=2sinB z+z1=2sinC 20
z+z1=2sinC 20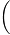 x+x1
x+x1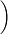 =21
=21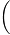 y+y1
y+y1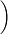 =29
=29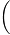 z+z1
z+z1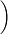 20sinA=21sinB=29sinC202+212=292sinA=2920
20sinA=21sinB=29sinC202+212=292sinA=2920 sinB=2921
sinB=2921 sinC=1x=tan2A=sinA1+cosA=29201+2921=52y=tan2B=sinB1+cosB=29211+2920=73z=tan2C=1
sinC=1x=tan2A=sinA1+cosA=29201+2921=52y=tan2B=sinB1+cosB=29211+2920=73z=tan2C=1 x
x y
y z
z =
=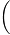 52
52 73
73 1
1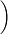
由於
 y
y z
z  x
x y
y z
z =
= −52
−52 −73
−73 −1
−1
回復 1# Superconan 的帖子
老師您好,我有去考試,印象中…填充3 題目是:已知三「正」數
非常感謝老師,辛苦把題目找出來分享。
回復 1# Superconan 的帖子
這家進去也是要用英文教數學嗎?不然怎麼一堆英文試題?社區高中用中文都不一定聽得懂了,還英文,看來挑戰很大喲
另外,剛官方只公告英文科的選擇題和答案,看來不會有數學科的試題了,您這份試題彌足珍貴啊
回復 5# thepiano 的帖子
回鋼琴老師:這間的簡章有寫是為了國際文憑課程,錄取老師要公費進修。這個課程是學生可以選擇加入,所以應該不是所有學生都用英文上。不過對於這間有疑問的是,最後30分的素養導向教案如何評分?如果寫出一份完整教案但其實跟素養關係不大會如何給分?另外想請教第七題
回復 6# jerryborg123 的帖子
令積分0~2 f(x)dx=Lf(x)=Lx^3-3x^2+2Lx-10
積分0~2後=L
得到L=4
把A(X-H)^3+P(X-H)+K=AX^3-3AHX^2+(3AH+P)X+(-AH-PH+K)
比較係數得到
A=4,P=29/4,H=1/4,K=-65/8
回復 4# iamagine 的帖子
謝謝您,已更正回復 5# thepiano 的帖子
謝謝鋼琴老師,這樣就不枉費我花了10多個小時還原題目,
然後心滿意足去睡覺時發現...
忘記報名桃園聯招... [quote]原帖由 [i]Superconan[/i] 於 2020-5-25 22:20 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=21271&ptid=3334][img]https://math.pro/db/images/common/back.gif[/img][/url]
謝謝鋼琴老師,
這樣就不枉費我花了10多個小時還原題目,
然後心滿意足去睡覺時發現...
忘記報名桃園聯招... [/quote]
記憶力要夠好~英文能力也要不錯 [quote]原帖由 [i]jerryborg123[/i] 於 2020-5-25 15:27 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=21268&ptid=3334][img]https://math.pro/db/images/common/back.gif[/img][/url]
回鋼琴老師:這間的簡章有寫是為了國際文憑課程,錄取老師要公費進修。這個課程是學生可以選擇加入,所以應該不是所有學生都用英文上。不過對於這間有疑問的是,最後30分的素養導向教案如何評分?如果寫出一份完整教案但其實跟 ... [/quote]
考卷它有說要用素養導向寫嗎?
若單只寫出教案,應該還是會有些基本的得分
至於如何扯到素養,就要靠想像力,沒制式答案
但還是可以從核心素養的三面九項下筆去寫
回復 11# Ellipse 的帖子
橢圓老師好:其實我英文不太好,剛好用兩個女生的名字找到試題。
您問的教案,我有補充在 pdf 裡面了
回復 1# Superconan 的帖子
初試分數58分 10-(b)想討論這題英文名詞上的問題
題目是用 face 而不是 plane
我的認知是前者代表該物體的面(不會無限延伸),後者是一般數學上講的平面
所以答案應該只有一個
可惜學校沒公布正解,有人知道什麼狀況下會不公布正解嗎?
想請教計算8
想請教計算8 除了假設3次多項式硬爆之外,有沒有其他的做法回復 15# z78569 的帖子
第8題 x2+1
x2+1
 x2+x+1
x2+x+1 q
q x
x +
+ ax3+bx2+cx+d
ax3+bx2+cx+d x2=−10=−ax−b+cx+da=c
x2=−10=−ax−b+cx+da=c b=d x2000−1=
b=d x2000−1= x2+1
x2+1
 x2+x+1
x2+x+1 q
q x
x +
+ ax3+bx2+ax+b
ax3+bx2+ax+b x=
x= =2−1+
=2−1+ 3i
3i 2−1=a+b
2−1=a+b 2+a
2+a +b=a+b
+b=a+b 2+a
2+a −1−
−1− 2
2 +b=
+b= b−a
b−a
 2+bb=−1
2+bb=−1 a=−2
a=−2好像差不多
回復 16# thepiano 的帖子
好的 作法差不多!感謝thepiano老師
回復 14# jerryborg123 的帖子
您可以打電話去反應之前中一中和北科附工都是有反應才有
[url]https://math.pro/db/thread-1184-1-1.html[/url]
回復 7# yi4012 的帖子
請問老師為什麼積分後得到L? L不是一個定值嗎?回復 19# jerryborg123 的帖子
任意函數從A積到B會變成常數比如:
從0~2 X^2 dX=1/3*X^3(0~2)=8/3
令從0~2 F(X)的積分值為L帶入後
f(x)=Lx^3-3x^2+Lx-10,L為常數
再積分一次值會相同,解一元一次方程式
L=積分0~2 f(x)dx
=積分0~2 LX^3-3X^2+2LX-10 dx
=L/4*X^4-X^3+L*X^2-10X(0~2)
=4L-8+4L-20=L
L=4
代回去得到F(X)=4X^4-3X^2+8X-10
之後就是比較係數
頁:
[1]
2