分享手寫訂正,有錯誤還多請大家指教~
感謝版上大大分享填充13,16,17,19想法 > < !! [/quote]
[第10題修正]
求a的最大值應用柯西不等式
p+q+r=3
(p+q+r)(q+r+p)>=(pq+qr+pr)^2=9a^2
0<= a <=1 故最大值取1
回復 21# XINHAN 的帖子
您的柯西不對吧? [quote]原帖由 [i]thepiano[/i] 於 2020-5-6 08:40 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=21129&ptid=3318][img]https://math.pro/db/images/common/back.gif[/img][/url]您的柯西不對吧? [/quote]
我發現問題了,抱歉抱歉,謝謝鋼琴大大指正 [quote]原帖由 [i]thepiano[/i] 於 2020-5-6 08:40 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=21129&ptid=3318][img]https://math.pro/db/images/common/back.gif[/img][/url]
您的柯西不對吧? [/quote]
我剛剛趕快修正一下
3a = pq+qr+pr = 1/2 * [(p+q+r)^2 - (p^2+q^2+r^2)] = 1/2 * [9 - (p^2+q^2+r^2)] <= 1/2 * [9 - 3] = 3
a <= 1
註:
(p^2+q^2+r^2)(1^2+1^2+1^2) >= (p+q+r)^2 = 9
p^2+q^2+r^2 >= 3
-(p^2+q^2+r^2) <= -3
等腰直角三角形內接正方形求面積
等腰直角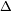 ABC
ABC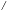 A=90
A=90
 3CG
3CG (朋友問的105北區第二次學測模擬考的題目,解完放上來分享一下。)
解答:
令 D(0,0), C(2,0), A(0,2), G(a,b),則
E(-b,a) → F(a-b, a+b)
因為 F(a-b, a+b) 位在直線AC: x+y=2 上,
所以 (a-b)+(a+b)=2,得 a=1,
→ G(1,b)、E(-b,1)
因為 GC : BE = 1:√3,
所以 BE^2 = 3 GC^2
→ (b-2)^2 + 1^2 = 3(1^2 + b^2)
→ b^2 + 2b -1 =0
→ (b+1)^2 = 2
→ b = -1 +√2
所求正方形面積 = 1^2 + b^2 = 4-2√2
111.7.29
補充模擬考題目和答案
頁:
1
[2]