請教一題極限
計算
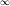 n
n
 n+1
n+1
 n+2
n+2



 n+n
n+n
 1n
1n 回復 1# eyeready 的帖子

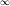 n
n
 n+1
n+1
 n+2
n+2



 n+n
n+n
 1n=limn
1n=limn
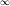
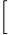
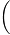 1+n1
1+n1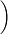
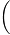 1+n2
1+n2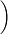



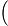 1+nn
1+nn
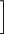 1n=elimn
1n=elimn
 1n
1n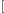 ln
ln 1+1n
1+1n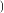 +ln
+ln 1+2n
1+2n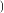 +
+

 +ln
+ln 1+nn
1+nn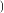
 =e
=e 12lnxdx=eln4−1=e4
12lnxdx=eln4−1=e4回復 2# thepiano 的帖子
感謝^ ^!頁:
[1]

 n
n
 n+1
n+1
 n+2
n+2



 n+n
n+n
 1n
1n 
 n
n
 n+1
n+1
 n+2
n+2



 n+n
n+n
 1n=limn
1n=limn
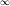
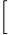
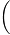 1+n1
1+n1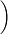
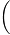 1+n2
1+n2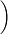



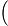 1+nn
1+nn
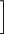 1n=elimn
1n=elimn
 1n
1n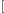 ln
ln 1+1n
1+1n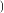 +ln
+ln 1+2n
1+2n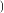 +
+

 +ln
+ln 1+nn
1+nn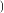
 =e
=e 12lnxdx=eln4−1=e4
12lnxdx=eln4−1=e4