97台中一中
翻到 多年前 老題目貼上來 參考一下 附上以前的討論,爬文後若還有問題再來發問
h ttp://forum.nta.org.tw/examservice/showthread.php?t=46779 (連結已失效)
103.9.8補充
階梯的理論
[url]http://www.shiner.idv.tw/teachers/viewtopic.php?f=53&p=9960#p9960[/url] [quote]原帖由 [i]bugmens[/i] 於 2012-5-5 07:04 PM 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=5414&ptid=1344][img]https://math.pro/db/images/common/back.gif[/img][/url]
附上以前的討論,爬文後若還有問題再來發問
[url=http://forum.nta.org.tw/examservice/showthread.php?t=46779]http://forum.nta.org.tw/examservice/showthread.php?t=46779[/url] [/quote]想請教第17題,
畫成像階梯狀的理論基礎是什麼?
有其他解法嗎?
97 台中一中
好老的考古題了第16 題
求組合數
怎麼算, 感謝喔
回復 4# l123eric 的帖子
cplee8tcfsh 老師已解,如果需要更多補充說明可見彬爸的
這篇【七進位在組合數求餘數的實例應用】[url]http://cplee8tcfsh.blogspot.tw/2008/06/7-decimal.html[/url]
回復 4# l123eric 的帖子
填充題第16題。用同餘理論。我也是研究好久,絕對不可能暴力法展開。
因為2008, 1234數字太大了。
[[i] 本帖最後由 shingjay176 於 2014-3-20 12:31 PM 編輯 [/i]]
回復 6# shingjay176 的帖子
也來補一個解法,基本精神是大同小異的,只是選擇對 ! 遞降設
 b
b 對所有正整數
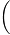
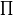 nk=1k
nk=1k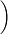

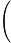
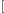 7n
7n k=17k
k=17k
 (−1)a
(−1)a b! (Mod 7)
b! (Mod 7) (7a
(7a a!)
a!)(證明要用到
 −1
−1則
 7286
7286 286!p1234
286!p1234 7176
7176 176!
176! p774
p774 7110
7110 110!=p2008
110!=p2008 286!p1234
286!p1234 176!
176! p774
p774 110!=
110!=

 =p2008p286p40p5p1234p176p25p3p774p110p15p2
=p2008p286p40p5p1234p176p25p3p774p110p15p2再利用同餘則得
 6!
6! 6!
6! (−5!)
(−5!) 12!
12! (−1!)
(−1!) (−4!)
(−4!) 3!
3! 4!
4! (−5!)
(−5!) 1!
1! 2!
2! 6 (Mod 7)
6 (Mod 7)回復 1# cplee8tcfsh 的帖子
請教第2題(簡答不太懂),感謝。回復 8# mathca 的帖子
第 2 題從
 1
1 2
2 4
4 5
5 6
6 7
7 8
8 9
9 0
0
[解答]
{0,6,9}
{1,4,7}
{2,5,8}
千百個十
千位有 8 種填法,百位有 9 種填法,個位有 2 種填法
以上 8 * 9 * 2 種填法中的任一種,其千位數字 、百位數字和個位數字之和除以 3 的餘數只有 0、1、2 這 3 種情形
不管餘多少,十位數字都有 3 種填法
故所求 = 8 * 9 * 2 * 3 個
回復 9# thepiano 的帖子
感謝。原來沒有3,看太快。回復 1# cplee8tcfsh 的帖子
請教第11題,感謝。回復 11# mathca 的帖子
第 11 題如圖,若

 ∠ACE=40
∠ACE=40
以一個正 24 邊形的頂點任取三點所組成的三角形中,三內角均大於30度的三角形有幾個。
小弟想法是把題目看成24個區間
把這24個區間分成三大部分 每大部分要有至少5個區間(滿足內角大於30度)
得到X+Y+Z=9 共有55種
請問這樣的想法錯在哪 或者我少考慮哪些條件
答案是440
回復 13# satsuki931000 的帖子
參考[url]http://www.shiner.idv.tw/teachers/viewtopic.php?f=53&t=1510[/url]
回復 14# thepiano 的帖子
懂了 謝謝鋼琴老師 想請教第12題,剛好在寸絲講義上有看到,但不曉得為何要這樣解上面是寫成令x=a+b,y=a-b去變數變換解得
想請問為何要這樣做假設呢? 謝謝各位老師
回復 16# plpl69541 的帖子
小弟認為變數變換這東西完全因人而異沒有一定要用哪個變換法才是對的 單純想不想的到 好不好處理而已
以這題來說 小弟我直觀就是直接做
就當作一般的聯立方程式去解看看
整理出來化簡後可以得到5次方二項式定理展開的樣子
頁:
[1]