max100 發表於 2011-7-29 23:03
100松山家商第二次代理
如附件!
mathca 發表於 2015-12-11 18:43
回復 1# max100 的帖子
請教第4題,感謝。
thepiano 發表於 2015-12-11 20:34
回復 2# mathca 的帖子
第4題
設正實數
a之小數部分為
b,且
a2+2b2=15,則
a+2b=[u] [/u]。
[解答]
0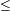 b
b 10
10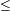 2b2
2b2 20
20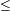 15−a2
15−a2 213
213 a2
a2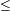 15b=a−3a2+2
15b=a−3a2+2 a−3
a−3 2=15
2=15





mathca 發表於 2015-12-11 21:34
回復 3# thepiano 的帖子
感謝。
satsuki931000 發表於 2020-8-20 14:19
請教填充2
koeagle 發表於 2020-8-20 15:50
回復 5# satsuki931000 的帖子
2.
在空間中,通過一直線:
x=3+t,
y=3−t,
z=0(
t為任意實數),且與球面:
x2+y2+z2−2x+2y−4=0相切的平面有兩個,其方程式分別為[u] [/u]。
[解答]
球面:
(x−1)2+(y+1)2+z2=6,球心
O(1 −1
−1 0)
0) ,半徑
r= 6
6
將直線改寫成兩面式:
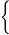 x+y−6=0z=0
x+y−6=0z=0 ,令切平面為
(x+y−6)+kz=0
相切:
d=r
 6=
6= 2+k2
2+k2 1−1−6
1−1−6
 k=
k= 2
2
切平面方程式:
x+y 2z−6=0
2z−6=0。
頁:
[1]
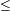 b
b 10
10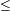 2b2
2b2 20
20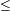 15−a2
15−a2 213
213 a2
a2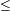 15b=a−3a2+2
15b=a−3a2+2 a−3
a−3 2=15
2=15





 −1
−1 0)
0)  6
6 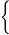 x+y−6=0z=0
x+y−6=0z=0 
 6=
6= 2+k2
2+k2 1−1−6
1−1−6
 k=
k= 2
2 2z−6=0
2z−6=0