100鳳山高中
今天考完鳳山高中,暈...總共12題,我把記得的部分打在WORD檔
題號跟題序跟正式版會有出入,不過題意89不離10
想要先睹為快的網友請享用
另外想請問 #2,4,5,6,請大家幫忙解惑,謝謝!!
感謝版主協助加附檔
追加鳳中一題,數據忘記,但類型同100中壢高中填充第8
[url=https://math.pro/db/thread-1119-1-1.html]https://math.pro/db/thread-1119-1-1.html[/url]
8. 設 f,g為可微分函數,且f(x+2y)=f(x)+g(y)
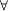 x
x y
y R
R 試問:若 f(0)=1, f'(0) =2, 求 g(5)
看到這題真的快哭出來了,明明有看過,寫考古題的時候就不會寫,當下當然想不出來
剛剛才想到怎麼算= =|||
[[i] 本帖最後由 紫月 於 2011-6-18 11:07 PM 編輯 [/i]] 8.
f,g可微 f(x+2y)=f(x)+g(y),f(0)=1,f`(0)=2,求g(10) 對上式兩邊同對x 微分,可得f'(x)都是定值...因為f'(0)=2,所以最後可令f(x)=ax+b.......代入原式...最後可得g(10)=40 #4
100彰女填充第二部分第11題
[url=https://math.pro/db/thread-1113-2-2.html]https://math.pro/db/thread-1113-2-2.html[/url]
[[i] 本帖最後由 老王 於 2011-6-19 10:20 PM 編輯 [/i]]
回復 5# 老王 的帖子
#5抱歉我沒有打清楚,a、b是歪斜,求最小體積沒有錯 #2將
 x2−(4−m)x+1=0
x2−(4−m)x+1=0 另一方面
 y4−(4m−m2)y2+m2=0
y4−(4m−m2)y2+m2=0 y12y22=m2
y12y22=m2因為m是正數,以及交點在第一象限,所以
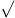 6m−m2
6m−m2 中點在y=x上
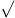 6m−m2
6m−m2  m2−7m+8=0
m2−7m+8=0  17
17 orm=27−
orm=27− 17
17 但是m要小於4
所以
 17
17 回復 1# 紫月 的帖子
當 0
0四面體體積不就
 0
0題目沒有漏掉條件嗎?
[img]http://i.imgur.com/fOnWa.png[/img]
回復 9# weiye 的帖子
這一題是求最大體積才對考試的時候 我沒算出來
後來我才想到 我算 2sqrt(3)/27 不知道對不對?
[[i] 本帖最後由 Herstein 於 2011-6-20 01:47 AM 編輯 [/i]] #5
假設AB=a,CD=b,AC=BC=AD=BD=1
取AB中點M,CM和DM都垂直AB
所以AB垂直平面CDM
將四面體分成A-CDM和B-CDM
體積為
 21b
21b
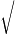 1−4a2−4b2
1−4a2−4b2 a
a 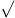 4−a2−b2
4−a2−b2 令
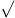 4−a2−b2
4−a2−b2 可知若
 4
4算幾不等式
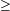 3
3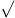 3a2b2c2
3a2b2c2  98
98 3
3 體積最大值
 3
3 請問第6,7,9題.謝謝
100鳳山高中公告版
as title學校在7月2日公佈.....囧.....
還好被我抓到
如附件
請各位參照! 我想問公佈板的題目 第3題 感謝八神庵過了這麼久還記得去學校網站留意有沒有公佈題目
否則校方一拿掉公告這份題目就失傳了
2.
袋中有1,2,...,9號球各一個,每次自袋中取出一球,取後放回,共取n次,n次和為偶數的機率記為
求(1)

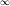 Pn=
Pn=不透明箱內有編號分別為1至9的九個球,每次隨機取出一個,紀錄其編號後放回箱內;以
求
(99鳳新高中,[url=https://math.pro/db/thread-974-1-2.html]https://math.pro/db/thread-974-1-2.html[/url])
[url=http://www.shiner.idv.tw/teachers/viewtopic.php?p=4089#p4089]http://www.shiner.idv.tw/teachers/viewtopic.php?p=4089#p4089[/url]
一袋中有5個球,分別寫上1、2、3、4、5號,今由其中任取一球記下其號碼後放回袋中,如此繼續n次,若
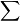
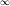 n=1(21−Pn)=
n=1(21−Pn)= (100中科實中,[url=https://math.pro/db/thread-1107-1-1.html]https://math.pro/db/thread-1107-1-1.html[/url])
3.
利用最小平方法得到二維數據
 y1)
y1) y2)
y2) yn)
yn) 另一組二維數據
 v1)
v1) v2)
v2) vn)
vn) 已知
 b
b c
c d
d e
e d
d [答案]
7.
求方程式
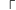


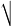 x+
x+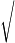 x+
x+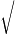 x+
x+

 +
+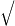 x+
x+ x=y
x=y x,y的非負整數解,其中共有2011個√,且√指正根而言。
Find all possible integer solutions for
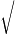 x+
x+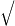 x
x

 (x+
(x+ x
x

 )=y
)=y 連結已失效h ttp://www.cs.cornell.edu/~asdas/imo/r41-50.html
補個類似題
試求方程
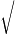 2+
2+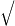 2+
2+

 +
+ 2+x
2+x 試求方程:
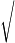 2+
2+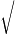 2+
2+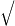 2+
2+ 2+x
2+x (初中數學競賽教程P353)
101.4.30補充
設
 3]=2
3]=2 5]=−3
5]=−3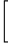
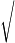 2010+
2010+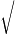 2010+
2010+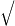 2010+
2010+ 2010+
2010+

 +2010
+2010
(其中共有2010個2010)
(建中通訊解題第82期)
[解答]
定義數列,
 2010+an
2010+an  2010
2010  44
44 a1
a1 45
45 45
45
 2055
2055
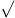 2010+a1
2010+a1
 2056
2056 46
46 45
45 a2
a2 46
46 繼續如此的步驟
 45
45 a3
a3 46
46 45
45 a4
a4 46
46



 45
45 a2010
a2010 46
46故所求
113.4.10補充
令
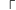


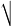 2024+
2024+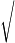 2024
2024

 +
+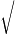 2024+
2024+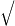 2024+
2024+ 2024
2024 註:
(113北一女中,[url]https://math.pro/db/viewthread.php?tid=3828&page=1#pid25679[/url]) 請教一下
這份考題有答案嗎?
小弟我沒找到,有的可以分享一下嗎?
謝謝! 老師您好,請問第10題應該要如何著手呢??
三正數a,b,c,a+b+c=3的那一題,謝謝老師。 [quote]原帖由 [i]bluewing[/i] 於 2011-7-14 10:54 AM 發表 [url=https://math.pro/db/redirect.php?goto=findpost&pid=4017&ptid=1151][img]https://math.pro/db/images/common/back.gif[/img][/url]
老師您好,請問第10題應該要如何著手呢??
三正數a,b,c,a+b+c=3的那一題,謝謝老師。 [/quote]
這裏有類題…還是謝謝這一版…。
[url=https://math.pro/db/thread-1128-1-1.html]https://math.pro/db/thread-1128-1-1.html[/url]
借用那邊算的結果答案為3/2…。
好像也可用猜的…a=b=c=1代入求解…。
[[i] 本帖最後由 peter579 於 2011-7-18 03:55 PM 編輯 [/i]] 請問#3(問迴歸直線方程式)的答案斜率不必分正負嗎? 不過我算出來的常數項也算錯就是了,所以想請教一下該怎麼算?
還有也想問一下#12的證明該怎麼寫,謝謝
[[i] 本帖最後由 pizza 於 2012-2-27 05:19 PM 編輯 [/i]]
回復 19# pizza 的帖子
第 3 題:設
 x2
x2



 xn
xn y2
y2



 yn
yn u2
u2



 un
un v2
v2



 vn
vn<<先來看看已知蝦咪>>
因為
所以 \overline{y}=a+b\overline{x} 且 \displaystyle b=r_{XY}\cdot\frac{S_y}{S_x}
<<再來看看最後是找出來蝦咪東西,寫過程的時候這一塊通常反而是會很後面才說~>>
|
| v 對 u 的迴歸直線必通過 (\overline{u},\overline{v}),
|
| 且其斜率為 \displaystyle r_{UV}\cdot\frac{S_v}{S_u}
|
└──────────────────────────<其實這塊只是在思考接下來要怎樣走~不用寫啦>
<<好吧,要把這兩者扯再一起了~>>
因為 u=c+dx,所以 \displaystyle \overline{u}=c+d\overline{x}\Rightarrow \overline{x}=\frac{\overline{u}-c}{d}
因為 v=e+fy,所以 \displaystyle \overline{v}=e+f\overline{y}\Rightarrow \overline{y}=\frac{\overline{v}-e}{f}
因為 \overline{y}=a+b\overline{x},所以 \displaystyle \frac{\overline{v}-e}{f}=a+b\left(\frac{\overline{u}-c}{d}\right) ───(*)
且
\displaystyle r_{UV}\cdot\frac{S_v}{S_u}=\frac{df}{|df|}r_{XY}\cdot\frac{|f|S_y}{|d|S_x}
\displaystyle =\frac{df}{|d|^2}\cdot r_{XY}\cdot\frac{S_y}{S_x}
\displaystyle =\frac{f}{d}\cdot b
<<再來招喚剛剛思考的那塊~>>
因為 v 對 u 的迴歸直線必通過 (\overline{u},\overline{v}),
且其斜率 \displaystyle r_{UV}\cdot\frac{S_v}{S_u}=\frac{f}{d}\cdot b
因此,v 對 u 的迴歸直線為
\displaystyle v-\overline{v}=\frac{f}{d}\cdot b(u-\overline{u})
\displaystyle \Rightarrow \frac{v-\overline{v}}{f}=\frac{b}{d}(u-\overline{u})
\displaystyle \Rightarrow \frac{(v-e)-(\overline{v}-e)}{f}=\frac{b}{d}\left((u-c)-(\overline{u}-c)\right)
\displaystyle \Rightarrow \frac{v-e}{f}-\frac{\overline{v}-e}{f}=\frac{b(u-c)}{d}-\frac{b(\overline{u}-c)}{d}
將(*)帶入可得
\displaystyle \Rightarrow \frac{v-e}{f}-a=\frac{b(u-c)}{d}
\displaystyle \Rightarrow \frac{v-e}{f}=a+b\cdot\frac{u-c}{d}
結束。
然後,下次如果是考填充題,那就~
把 \displaystyle u=c+dx, v=e+fy\Rightarrow x=\frac{u-c}{d}, y=\frac{v-e}{f} 帶入 y=a+bx
即可得 \displaystyle \frac{v-e}{f}=a+b\cdot\frac{u-c}{d}
回復 19# pizza 的帖子
第 12 題:已知 p(0)=a_0 為奇數,且 p(1)=a_n+a_{n-1}+\cdots+a_0 亦為奇數,
假設 p(x)=0 有整數根 \alpha,
若 \alpha 為偶數,則
p(\alpha)=a_n\alpha^n+a_{n-1}\alpha^{n-1}+\cdots+a_1\alpha+a_0\equiv a_0\equiv 1\pmod{2}
\Rightarrow p(\alpha)\not\equiv0\pmod2 此與 p(\alpha)=0 互相矛盾。
若 \alpha 為奇數,則
p(\alpha)=a_n\alpha^n+a_{n-1}\alpha^{n-1}+\cdots+a_1\alpha+a_0
\equiv a_n\cdot1^n+a_{n-1}\cdot1^{n-1}+\cdots+a_1\cdot1+a_0
\equiv a_n+a_{n-1}+\cdots+a_0 \equiv 1\pmod{2}
\Rightarrow p(\alpha)\not\equiv0\pmod2 此與 p(\alpha)=0 互相矛盾。
因此,p(x)=0 既無偶數根,亦無奇數根,
可得 p(x)=0 無整數根。
頁:
[1]
2