小弟我獲益良多
冒昧請教一下,第一題答案是3,對否?
謝謝
回復 23# t3712 的帖子
第 1 題:設 B
B C
C D
D  PB
PB PC
PC PD
PD解答:
設
 )(x−
)(x−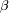 )(x−
)(x−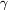 )(x−
)(x−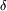 )
)  PB
PB PC
PC PD=
PD= i−
i−


 i−
i−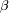


 i−
i−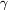


 i−
i−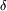


 i−
i−

 i−
i−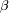

 i−
i−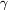

 i−
i−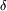


 f(i)
f(i) =
= i4−i2+1
i4−i2+1 =3
=3 因為AC是直徑,所以

 AB
AB =
= AB
AB
 2
2 以及

 AD
AD =
= AD
AD
 2
2 就會得到
 AB
AB
 2+25AB
2+25AB
 AD
AD =
= AB
AB
 2
2
 AD
AD +25
+25 AD
AD
 2=
2= AD
AD
 2
2整理得

 AD
AD =−51
=−51 AB
AB
 2=−
2=− AD
AD
 2
2又AC=2得到
 AB
AB
 2+215AB
2+215AB
 AD
AD +425
+425 AD
AD
 2
2令
 AD
AD
 2=K
2=K 則
 AB
AB
 2=5K
2=5K AB
AB
 AD
AD =−K
=−K  K=52
K=52於是
 BD
BD
 2
2  AD
AD
 2−2AB
2−2AB
 AD
AD +
+ AB
AB
 2
2 最後得到
 5
5 假設AC與BD的交點為O
假設t*向量AC=向量AO=t*(3/2)*向量AB+t*(5/2)向量AD (t是實數)
因為A-O-C ,所以t*(3/2)+t*(5/2)=1 ,t=1/4
又AC=2,所以AO=2*(1/4)=1/2 ,CO=3/2
且向量AO=(1/4)*向量AC=(3/8)*向量AB+(5/8)*向量AD
所以DO:BO=3:5,令DO=3k,BO=5k(k是正實數)
由圓冪定理得 AO*CO=DO*BO,(1/2)*(3/2)=(3k)*(5k)
解得k=5^0.5/10 ,所求=BD=8k=4*5^0.5/5 填充第九題
答案是a=9/4 b=-19/12 嗎
回復 27# satsuki931000 的帖子
Yes頁:
1
[2]